Pont 1.1 Halmazok
A matematikában egy halmaz egy objektumok gyűjteménye, amelyeket elemeknek nevezünk. Általában a halmazokat nagybetűkkel, az elemeket pedig kisbetűkkel jelöljük. Ha \(A\) egy halmaz, és \(a\) az \(A\) eleme, akkor \(a\in A\)-t írunk. Ha \(a\) nem az \(A\) eleme, akkor \(a\notin A\)-t írunk. Most azzal a problémával foglalkozunk, hogyan lehet egy halmazt létrehozni.
Halmazok felsorolással. Ha van egy halmaz, amely bizonyos elemeket tartalmaz, akkor ezeket az elemeket kapcsos zárójelbe tesszük. Például, ha \(A\) egy halmaz, amely 1, 2 és 3 elemeket tartalmaz, akkor \(A=\halmaz{1,2,3}\)-t írunk. Ez a jelölés nehezen használható, ha a megadott halmaz sok elemet tartalmaz. Ebben az esetben csak néhány (általában egymás utáni) elemet sorolunk fel úgy, hogy könnyen látható legyen, melyek a halmaz többi elemei. Például tegyük fel, hogy \(B\) egy halmaz, amely tartalmazza az 1 és 1000 közötti egész számokat. Itt \(B=\halmaz{1,2,3,\ldots,1000}\)-t írunk. Ha \(C\) a 1 és 99 közötti páratlan egész számokat tartalmazó halmaz, akkor \(C=\halmaz{1,3,5,\ldots,99}\text{.}\) Lehetőség van néhány halmazcsalád megadására is, például
\begin{equation*}
D_1=\{1\}, D_k=\halmaz{1,3,\ldots,2k-1}\text{.}
\end{equation*}
Ebben az esetben
\(D_k\) az első
\(k\) pozitív páratlan egész számokat tartalmazó halmazt jelöli.
|
|
| \(k\) |
\(D_k\) |
|
|
| 1 |
\(\halmaz{1}\) |
|
|
| 2 |
\(\halmaz{1,3}\) |
|
|
| 3 |
\(\halmaz{1,3,5}\) |
|
|
| 4 |
\(\halmaz{1,3,5,7}\) |
|
|
Fontosabb/ismert halmazok. Vannak bizonyos gyakran használt halmazok, amelyeknek saját szimbólumaik vannak. Ezek a természetes számok halmaza, az egész számok halmaza, a racionális számok halmaza, a valós számok halmaza és a komplex számok halmaza. \(\mathbb{N}=\halmaz{1,2,3,\ldots}\text{,}\) a természetes számok halmaza. \(\mathbb{Z}=\halmaz{\ldots,-2,-1,0,1,2,\ldots}\text{,}\) az egész számok halmaza. \(\mathbb{Q}\text{,}\) a racionális számok halmaza. \(\mathbb{R}\text{,}\) a valós számok halmaza. \(\mathbb{C}\text{,}\) a komplex számok halmaza.
Halmazépítő jelölés. A halmazokat a úgynevezett halmazépítő jelölés segítségével is definiálhatjuk. Például vegyük a \(D_3=\halmaz{1,3,5}\) halmazt, ezt a halmazt sok különböző módon definiálhatjuk, például\
\begin{align*}
\halmaz{1,3,5}\amp =\halmazvonal{a}{(a-1)(a-3)(a-5)=0},\\
\halmaz{1,3,5}\amp =\halmazvonal{a}{a=2k-1, k\in\halmaz{1,2,3}},\\
\halmaz{1,3,5}\amp =\halmazvonal{a}{1\leq a\leq 5, \mbox{ és \(a\) páratlan} }\text{.}
\end{align*}
Használhatunk pontosvesszőt is a függőleges vonal helyett:
\begin{align*}
\halmaz{1,3,5}\amp =\halmazpont{a}{(a-1)(a-3)(a-5)=0},\\
\halmaz{1,3,5}\amp =\halmazpont{a}{a=2k-1, k\in\halmaz{1,2,3}},\\
\halmaz{1,3,5}\amp =\halmazpont{a}{1\leq a\leq 5, \mbox{ és \(a\) páratlan} }\text{.}
\end{align*}
Definiáljuk a pozitív páros számokat:
\begin{equation*}
\halmazvonal{2n}{n\in\mathbb{N}}\text{.}
\end{equation*}
A racionális számok halmaza definiálható az alábbi módon:
\begin{equation*}
\halmazvonal{a/b}{a,b\in\mathbb{Z}, b\neq 0}\text{.}
\end{equation*}
Néhány alapvető halmaz tulajdonságának tanulmányozásához néhány definíciót adunk meg. Először bevezetjük a számosság fogalmát.
Definíció 1.1.1.
Egy halmaz véges akkor, ha véges számú eleme van. Ha egy halmaz nem véges, akkor végtelen.
Most a véges halmazok számosságát vizsgáljuk. A végtelen halmazok számossága bonyolultabb, és ezt nem fogjuk megvitatni.
Definíció 1.1.2.
Legyen \(A\) egy véges halmaz. Számosság \(A\) esetében az \(A\) különböző elemeinek száma. Jelölés: \(|A|\text{.}\)
Például, a \(D_3\) halmaz számossága 3, és a \(\halmaz{1,2,3,6,7,8}\) halmaz számossága 6.
Definíció 1.1.3.
Legyen \(A\) és \(B\) két halmaz. A \(B\) halmaz részhalmaza \(A\)-nak, pontosan akkor ha \(B\) minden eleme \(A\) eleme. Jelölés: \(B\subseteq A\text{.}\)
Van egy különleges halmaz, amely minden halmaz részhalmaza, az úgynevezett üres halmaz. Ahogy a neve is sugallja, ez az a halmaz, amelynek nincs eleme, azaz a számossága 0. Az üres halmazt \(\emptyset\) jelöli.
Definíció 1.1.4.
Ha \(B\subseteq A\) és \(B\neq\emptyset, B\neq A\text{,}\) akkor \(B\) valódi részhalmaza \(A\)-nak.
Definíció 1.1.5.
Legyen \(A\) és \(B\) halmazok. A két halmaz egyenlő, ha \(A\subseteq B\) és \(B\subseteq A\text{.}\)
Ha összegyűjtjük az \(A\) összes részhalmazát egy új halmazba, akkor halmazok egy halmazát kapjuk. Az \(A\) összes részhalmazának halmazát hatványhalmaznak nevezzük, és \(\pow(A)\)-ként jelöljük. Összesen hány részhalmaza van \(A\)-nak? Más szavakkal, mi \(|\pow(A)|\) (az \(A\) hatványhalmazának számossága)? Gondoljunk arra, hogyan építenénk fel egy részhalmazt. Minden egyes \(A\)-beli elemnél el kell döntenünk, hogy belefoglaljuk-e az elemet a részhalmazunkba. Minden egyes \(n\) elemre 2 választási lehetőségünk van. Ezért a részhalmazok száma egyszerűen
\begin{equation*}
\prod_{k=1}^n 2 = 2\cdot 2\cdot \cdots 2\cdot 2 = 2^n.
\end{equation*}
Bevezetünk néhány műveletet halmazok között.
Definíció 1.1.6.
Legyen \(A\) és \(B\) halmaz. Az metszet \(A\) és \(B\) között a \(\halmazvonal{x}{ x\in A \mbox{ és } x\in B}\) halmaz. Jelölés: \(A\cap B\text{.}\)
Az úgynevezett Venn-diagramok gyakran hasznosak a halmazok esetében a helyzet jobb megértéséhez. A megfelelő terület árnyékolásával illusztráljuk
\(A\) és
\(B\) metszetét.
Legyen
\(A=\halmaz{1,2,3,4,5}\) és
\(B=\halmaz{3,4,5,6,7}\text{.}\) A két halmaznak a metszete az
\(A\cap B=\halmaz{3,4,5}\) halmaz.
Definíció 1.1.7.
Legyen \(A\) és \(B\) halmaz. Az unió \(A\) és \(B\) között a \(\halmazvonal{x}{x\in A \mbox{ vagy } x\in B}\) halmaz. Jelölés: \(A\cup B\text{.}\)
A kapcsolódó Venn-diagram a következő.
Legyen
\(A=\halmaz{1,2,3,4,5}\) és
\(B=\halmaz{3,4,5,6,7}\text{.}\) E két halmaz uniója a
\(A\cup B=\halmaz{1,2,3,4,5,6,7}\) halmaz. Könnyen látható, hogy az alábbi tulajdonságok érvényesek:
\(A\cap B=B\cap A\) és
\(A\cup B=B\cup A\text{.}\) Ez nem igaz a két halmaz különbségére.
Definíció 1.1.8.
Legyenek \(A\) és \(B\) halmazok. A különbség \(A\) és \(B\) között a \(\halmazvonal{x}{ | x\in A \mbox{ és } x\notin B}\) halmaz. Jelölés: \(A\setminus B\text{.}\)
Az
\(A\setminus B\) művelethez tartozó Venn-diagram:
A különbség megértéséhez
\(A\setminus B\) és
\(B\setminus A\) között rajzoljuk a
\(B\setminus A\) Venn-diagramját is:
Ismét legyen
\(A=\halmaz{1,2,3,4,5}\) és
\(B=\halmaz{3,4,5,6,7}\text{.}\) Ekkor kapjuk, hogy
\begin{align*}
A\setminus B \amp =\halmaz{1,2},\\
B\setminus A \amp =\halmaz{6,7}\text{.}
\end{align*}
Most bevezetjük a halmazok szimmetrikus különbségét (vagy szimmetrikus differencia).
Definíció 1.1.9.
Legyenek \(A\) és \(B\) halmazok. A szimetrikus különbség \(A\) és \(B\) között a \((A\cup B)\setminus(A\cap B)\) halmaz. Jelölés: \(A\triangle B\text{.}\)
Az
\(A\) és
\(B\) szimmetrikus különbségének Venn-diagramja:
Példát adunk az
\(A=\halmaz{1,2,3,4,5}\) és
\(B=\halmaz{3,4,5,6,7}\) halmazok használatával. Megkapjuk, hogy
\begin{equation*}
A\triangle B=\halmaz{1,2,6,7}\text{.}
\end{equation*}
Végezetül definiáljuk egy halmaz komplementerét.
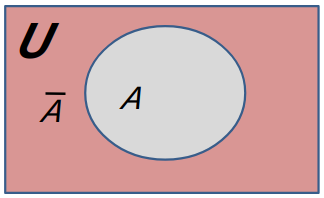
Definíció 1.1.10.
Legyen \(U\) egy halmaz (univerzumnak nevezve), és \(A\) az \(U\) egy részhalmaza. \(A\) komplementere azoknak az elemeknek a halmaza, amelyek \(U\)-ban vannak, de nem tartoznak \(A\)-hoz. Jelölés: \(\overline{A}\text{.}\)
A megfelelő Venn-diagram a következő.
Példaként vegyük a következő halmazokat \(U=\{1,2,3,4,5,6\}\) és \(A=\{1,3,5\}\text{.}\) \(A\) komplementere a \(\{2,4,6\}\) halmaz.
Van még egy mód a halmazok kombinálására, ami hasznos lesz számunkra: a Descartes szorzat, \(A \times B\text{.}\) Ez jól hangzik, de semmi olyat nem tartalmaz, amit még nem láttunk. Amikor egy függvényt ábrázolunk a kalkulusban, a megfelelő Descartes síkban ábrázoljuk. Ez a valós számok összes rendezett párjának halmaza \((x,y)\text{.}\) Ezt bármely pár halmazra megtehetjük, nem csak a valós számok esetében.
Definíció 1.1.11.
Adott \(A\) és \(B\) halmazok, legyen
\begin{equation*}
A \times B = \{(x,y) \st x \in A \wedge y \in B\}\text{,}
\end{equation*}
amely az összes rendezett párt tartalmazza \((x,y)\text{,}\) ahol \(x\) az \(A\) eleme, és \(y\) a \(B\) eleme. Az \(A \times B\)-t Descartes szorzatnak nevezzük \(A\) és \(B\) esetében.
Az első koordináta az első halmazból, a második koordináta a második halmazból származik. Néha szeretnénk a halmaznak önmagával vett Descartes szorzatát venni, ami: \(A \times A = \{(a,b) \st a, b \in A\}\) (ezt a halmazt \(A^2\) -ként is írhatjuk). Három vagy több halmaz Descartes szorzatát is vehetjük, rendezett hármasokat, vagy négyeseket, és így tovább kapunk.
Feladatok Feladatok
1.
Legyen \(A=\halmaz{3,4,6,7,8},B=\halmaz{2,4,5,6,8}\) és \(C=\halmaz{1,2,4,5,8}\text{.}\) Mik a \((A\setminus B)\cup(C\cap B)\) halmaz elemei?
2.
Legyen \(A=\halmaz{1,3,4,6,7},B=\halmaz{2,4,5,6,8}\) és \(C=\halmaz{1,3,4,5,8}\text{.}\) Mik a \((A\cap B)\setminus(C\cap B)\) halmaz elemei?
3.
Legyen \(A=\halmaz{1,3,4,6,7},B=\halmaz{2,4,6,8}\) és \(C=\halmaz{1,3,4,8}\text{.}\) Mik a \((A\setminus B)\cup(C\setminus B)\) halmaz elemei?
4.
Sorold fel a következő halmazok összes elemét:
(a) \(\halmazvonal{3k+1}{k\in\halmaz{2,3,4}}\text{,}\)
(b) \(\halmazvonal{k^2}{ k\in\halmaz{-1,0,1,2}}\text{,}\)
(c) \(\halmazvonal{u-v}{u\in\halmaz{3,4,5}, v\in\halmaz{1,2}}\text{.}\)
5.
A halmazépítő jelölést használva adjuk meg az alábbi halmazokat!
(a) \(\halmaz{2,4,6,8,10}\text{,}\)
(b) \(\halmaz{1,4,9,16,25}\text{,}\)
(c) \(\halmaz{1,\frac{1}{2},\frac{1}{4},\ldots, \frac{1}{2^k}, \ldots}\text{,}\)
(d) Az 1 és 2 közötti racionális számok halmaza.
6.
Adjuk meg a következő halmazokhoz tartozó Venn-diagramokat!
(a) \((A\cap B)\cup C\text{,}\)
(b) \((A\setminus B)\cup(A\setminus C)\text{,}\)
(c) \((A\cup B)\cap C\text{,}\)
(d) \((A\cap B)\cup(B\cap C)\cup(A\cap C)\text{,}\)
(e) \(\left((A\cap B)\setminus C\right)\cup \left((A\cap C)\setminus B\right)\cup \left((B\cap C)\setminus A\right)\text{,}\)
(f) \((A\setminus B)\cup(B\setminus C)\cup(C\setminus A)\text{.}\)
7.
Adjunk meg olyan \(A,B\) és \(C\) halmazokat, amelyekre igazak az alábbi számossági feltételek:
\begin{equation*}
|A\cap B\cap C|=2\text{,}
\end{equation*}
\begin{equation*}
|A\cap B|=|A\cap C|=|B\cap C|=2\text{,}
\end{equation*}
\begin{equation*}
|A|=|B|=|C|=4\text{.}
\end{equation*}
8.
Adjunk meg olyan \(A,B\) és \(C\) halmazokat, amelyekre igazak az alábbi számossági feltételek:
\begin{equation*}
|A\cap B\cap C|=2\text{,}
\end{equation*}
\begin{equation*}
|A\cap B|=2, |A\cap C|=2, |B\cap C|=3\text{,}
\end{equation*}
\begin{equation*}
|A|=4, |B|=5, |C|=6\text{.}
\end{equation*}
9.
Legyen \(A = \{1,2\}\) és \(B = \{3,4,5\}\text{.}\) Határozzuk meg \(A \times B\) és \(A \times A\) halmazokat. Hány elem lesz \(B \times B\)-ben?
10.
Legyen \(X = \{n \in \N \st 10 \le n \lt 20\}\text{.}\) Keressünk példákat olyan halmazokra, amelyek a következő tulajdonságokkal rendelkeznek, és nagyon röviden magyarázzuk el, miért működnek a példák.
Egy \(A \subseteq \N\) halmaz, amelyre \(|A| = 10\) és \(X \setminus A = \{10, 12, 14\}\text{.}\)
Egy \(B \in \pow(X)\) halmaz \(|B| = 5\) tulajdonsággal.
Egy \(C \subseteq \pow(X),\) amire \(|C| = 5\text{.}\)
Egy \(D \subseteq X \times X\) halmaz, amelyre \(|D| = 5\)
Egy \(E
\subseteq X\) úgy, hogy \(|E| \in E\text{.}\)
11.
Határozd meg az alábbi halmazok számosságát.
\(A = \{3,4,\ldots, 15\}\text{.}\)
\(B = \{n \in \N \st 2 \lt n \le 200\}\text{.}\)
\(C = \{n \le 100 \st n \in \N \wedge \exists m \in \N (n = 2m+1)\}\text{.}\)
12.
Bármely \(A\) és \(B\) halmaz esetén, definiáljuk \(AB = \{ab \st a\in A \wedge b \in B\}\text{.}\) Ha \(A = \{1,2\}\) és \(B = \{2,3,4\}\text{,}\) mivel egyenlő \(|AB|\text{?}\) Mivel egyenlő \(|A \times B|\text{?}\)