Pont 6.1 Függvények tulajdonságai
Megfigyelhetjük, hogy egyes függvények gráfikonjainak ábrázolása egyszerűbb feladat, ami a gráfikon bizonyos szimmetria tulajdonságából fakad. A gráfikon lehet szimmetrikus az \(y\)-tengelyre, ami azt jelenti, hogy egy \((x,f(x))\) pont esetén \((-x,f(x))\) is rajta van a függvény görbéjén, azaz \(f(-x)=f(x)\text{.}\) Egy másik szimmetria lehetőség az origóra nézve szimmetrikus függvények esete, ekkor egy \((x,f(x))\) pont esetén \((-x,-f(x))\) is rajta van a függvény görbéjén, azaz \(f(-x)=-f(x)\text{.}\) Erre vonatkozóan tekintjük a következő definíciót.
Definíció 6.1.1.
Ha \(f(x)=f(-x)\) minden \(x\)-re az \(f\) értelmezési tartományában, akkor \(f\) páros függvény. A páros függvény az \(y\)-tengelyre szimmetrikus.
Ha \(f(-x)=-f(x)\) minden \(x\)-re az \(f\) tartományában, akkor \(f\) páratlan függvény. A páratlan függvény az origó körül szimmetrikus.
Más esetben is előfordul, hogy a függvény képe egyszerűbben vizsgálható, amikor egy adott intervallumon elegendő ismerni a függvényt és ennek ismétlődését látjuk, ezeket hívjuk periodikus függvényeknek.
Definíció 6.1.2.
Legyen \(D\) egy nem üres halmaz, és \(f : D \rightarrow \mathbb{R}\) egy függvény. Azt mondjuk, hogy az \(f\) függvény periódikus, ha létezik olyan \(0\lt p\) amire
\begin{equation*}
f(x+p)=f(x),\,\forall x\in D.
\end{equation*}
A sorozatoknál tanultakhoz analóg módon értelmezhetjük függvények monotonitását is.
Definíció 6.1.3.
Azt mondjuk, hogy egy \(f\) függvény monoton növekvő az \(I\) intervallumon, ha minden \(x_1,x_2\in I\) esetén \(f(x_1)\leq f(x_2)\) ha \(x_1\lt x_2\text{.}\)
Azt mondjuk, hogy \(f\) szigorúan monoton növekvő az \(I\) intervallumon, ha minden \(x_1,x_2\in I\) esetén, \(f(x_1)\lt f(x_2)\) ha \(x_1\lt x_2\text{.}\)
Azt mondjuk, hogy egy \(f\) függvény monoton csökkenő az \(I\) intervallumon, ha minden \(x_1,x_2\in I\) esetén, \(f(x_1)\geq f(x_2)\) ha \(x_1\lt x_2\text{.}\)
Azt mondjuk, hogy egy \(f\) függvény szigorúan csökkenő az \(I\) intervallumon, ha minden \(x_1,x_2\in I\) esetén, \(f(x_1)\gt f(x_2)\) ha \(x_1\lt x_2\text{.}\)
A következő fogalom, amit bevezetünk az a korlátosság.
Definíció 6.1.4.
Legyen \(D\) egy nem üres halmaz, és \(f : D \rightarrow \mathbb{R}\) egy függvény. Azt mondjuk, hogy \(f\) korlátos felülről, ha létezik \(M \gt 0\) úgy, hogy \(f(x)\leq M \, \forall x \in D.\)
Azt mondjuk, hogy \(f\) alulról korlátos, ha van olyan \(M \gt 0,\) hogy \(f (x) \geq -M \, \forall x \in D.\)
Végül azt mondjuk, hogy \(f\) korlátos, ha \(f\) felülről és alulról is korlátos. Azaz \(f\) korlátos, ha létezik \(M \gt 0,\) úgy, hogy \(|f(x)| \leq M \, \forall x \in D.\)
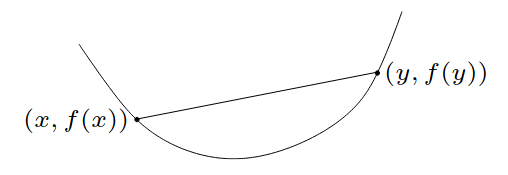
Függvények grafikonjával kapcsolatos fontos fogalom az úgynevezett konvexitás.
Definíció 6.1.5.
Legyen \(D\) egy nem üres halmaz, és \(f : D \rightarrow \mathbb{R}\) egy függvény.
- Azt mondjuk, hogy \(f\) konvex, ha \(\forall t\in [0,1]\) esetén
\begin{equation*}
f(tx+(1-t)y)\leq tf(x)+(1-t)f(y), \,\forall x,y\in D.
\end{equation*}
Azt mondjuk, hogy \(f\) konkáv, ha \(-f\) konvex.
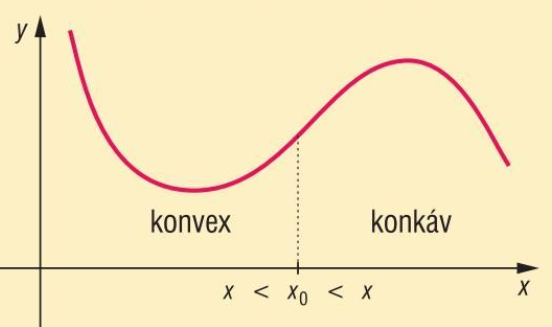
A periódikusság definíciójánál szereplő szinusz és koszinusz függvények ábrájánál megfigyelhetjük, hogy a függvények egyes intervallumokon konvexek, máshol pedig konkávok, azaz a függvények konvexitása változhat. Erre vonatkozik a következő definíció.
Definíció 6.1.6.
Egy \(x_0\) pontot az \(f\) függvény inflexiós pontjának nevezzük, ha a pontban a függvény konvexitása megváltozik.
Gyakorlati problémák esetében fontos szerepet játszanak az úgynevezett zérushelyek, lokális szélsőértékek, illetve a globális szélsőértékek. A későbbiekben meg fogjuk vizsgálni milyen módszerekkel tudjuk ezeket meghatározni bizonyos esetekben. Az alábbiakban bevezetjük ezeket a fogalmakat.
Definíció 6.1.7.
Legyen \(D\) egy nem üres halmaz, és \(f : D \rightarrow \mathbb{R}\) egy függvény, egy \(x_0\in D\) pontban a függvénynek zérushelye van, ha \(f(x_0)=0\text{.}\)
Definíció 6.1.8.
Az \(f\) függvénynek egy \((x_1,x_2)\) nyílt intervallum \(x_0\) pontjában lokális maximuma van, ha \(f(x_0)\geq f(x)\) minden \(x\in (x_1,x_2)\text{.}\)
Az \(f\) függvénynek egy \((x_1,x_2)\) nyílt intervallum \(x_0\) pontjában lokális minimuma van, ha \(f(x_0)\leq f(x)\) minden \(x\in (x_1,x_2)\text{.}\)