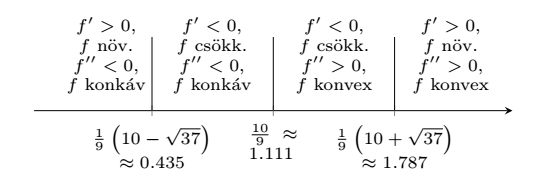Pont 10.1 Függvényvizsgálat
A 6. előadás folyamán megismerkedtünk függvények különféle tulajdonságaival: páros-páratlan, periódikus, monoton csökkenő-növekvő, konvex-konkáv, az inflexiós pontok fogalmával, lokális minimum-maximum definíciójával. Néhány egyszerű függvény esetében meg is néztük hogyan lehet ezeket a tulajdonságokat igazolni. Nem mentünk bele a részletekbe, hogy hogyan is lehetne ezt általánosabban vizsgálni, aminek az oka egyszerű: a függvény deriváltjainak vizsgálata nagyban segít megérteni a függvény viselkedését a fent említett tulajdonságokra nézve.
Definíció 10.1.1. Kritikus értékek és kritikus pontok.
Legyen \(f\) definiálva \(c\)-ben. A \(c\) értéket kritikusnak nevezzük ha \(f'(c)=0\) vagy \(f'(c)\) nem definiált.
Ha \(c\) egy kritikus értéke \(f\)-nek, akkor a \((c,f(c))\)-t kritikus pontnak nevezzük.
A józan ész azt mondja nekünk, hogy “a szélsőértékek vagy a végpontokon, vagy valahol a kettő között fordulnak elő.” A végpontoknál könnyen ellenőrizhetjük a szélsőértékeket, de végtelenül sok olyan pont van, ami a kettő között van.
Nézzük meg példán keresztül hogyan is működik ez a gyakorlatban.
Példa 10.1.3. Szélsőértékek meghatározása I.
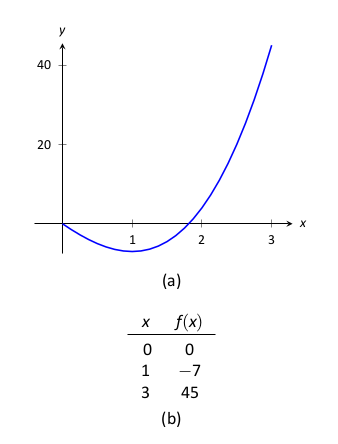
Határozzuk meg az \(f(x) = 2x^3+3x^2-12x\) függvény szélsőértékeit a \([0,3]\) intervallumon!
Megoldás.
Követjük a fenti módszer lépéseit. Kiszámítjuk \(f\) értékeit a végpontokban:
\begin{align*}
f(0)\amp=0\amp f(3)\amp=45\text{.}
\end{align*}
Meghatározzuk \(f\) kritikus értékeit a \([0,3]\) intervallumon. Kapjuk, hogy \(f'(x) = 6x^2+6x-12 = 6(x+2)(x-1)\text{;}\) azaz \(f\) kritikus értékei: \(x=-2\) és \(x=1\text{.}\) Az \(x=-2\) nincs a \([0,3]\) intervallumban, így ettől eltekintünk. Az \(f\) másik kritikus értéke már az intervallon belül helyezkedik el és itt: \(f(1) = -7\text{.}\)
A táblázat tartalmazza
\(f\) kiértékelését a “fontos”
\(x\) értékek esetében a
\([0,3]\) intervallumon. A maximum és minimum
\(f\) esetében adódik, mégpedig: a maximum érték
\(45\) a minimum pedig
\(-7\text{.}\)
Példa 10.1.4. Szélsőértékek meghatározása II.
Határozzuk meg az \(f\) függvény szélsőértékeit a \([-4,2]\) intervallumon, ahol
\begin{equation*}
f(x) = \begin{cases}(x-1)^2 \amp x\leq 0 \\ x+1 \amp x \gt 0\end{cases}\text{.}
\end{equation*}
Megoldás.
Először is jegyezzük meg, hogy \(f\) folytonos a \([-4,2]\) intervallumon (ellenőrizhető, hogy \(\lim\limits_{x\to 0}f(x) =f(0)\)).
Az \(f\) végpontjaiban tekintjük először a függvényt:
\begin{align*}
f(-4)\amp=25\amp f(2)\amp=3\text{.}
\end{align*}
Jöhetnek \(f\) kritkus értékei. Az \(f'\) ebben az esetben:
\begin{equation*}
f'(x) =\begin{cases}2(x-1) \amp x \lt 0 \\ 1 \amp x \gt 0\end{cases}\text{.}
\end{equation*}
Kiemeljük, hogy \(f\) az egész \([-4,2]\) intervallumon definiált, \(f'\) viszont nem, hiszen \(f\) deriváltja nem létezik \(x=0\)-ban. (Balról a derivált \(-2\)-höz tart; jobbról pedig \(1\)-hez.) Így az \(f\)-nek az \(x=0\) is kritikus értéke definíció szerint.
Tekintsük most az \(f'(x) = 0\) egyenletet. Amikor \(x \gt 0\text{,}\) \(f'(x)\) soha nem 0. Amikor \(x\lt 0\text{,}\) \(f'(x)\) szintén nem lehet 0.
A következő három fontos helyen kell megvizsgálnunk a függvényt:
\(x= -4, 2\) és
\(0\text{.}\) Kiszámítjuk
\(f\)-et ezeken a helyeken és kapjuk, hogy az értékek az adott sorrendben:
\(25\text{,}\) \(3\) és
\(1\text{.}\) A minimum
\(f\) esetében az intervallumon 1, a maximuma
\(f\)-nek pedig
\(25\text{.}\)
Példa 10.1.5. Szélsőértékek meghatározása III.
Határozzuk meg az \(f(x) = \cos\mathopen{}\left(x^2\right)\mathclose{}\) szélsőértékeit a \([-2,2]\) intervallumon!
Megoldás.
Ismét \(f\) végpontjaiban kezdjük a számolást: \(f(-2) = f(2) = \cos(4) \approx -0.6536\text{.}\) Jöhetnek az \(f\) függvény kritikus értékei.
A deriváltnál most alkalmaznunk kell a láncszabályt: \(f'(x) = -2x\sin\mathopen{}\left(x^2\right)\mathclose{}\text{.}\) Tekintsük az \(f'(x) = 0\) egyenletet és oldjuk meg \(x\)-re.
Adódik, hogy \(f'(x) = 0\) amikor \(x = 0\) vagy, ha \(\sin\mathopen{}\left(x^2\right)\mathclose{}=0\text{.}\) A \(\sin(t) = 0\) megoldásai a függvény periódikussága miatt: \(t = \ldots -2\pi, -\pi, 0, \pi, \ldots\) Azaz \(\sin\mathopen{}\left(x^2\right)\mathclose{} = 0\) amikor \(x^2 = 0, \pi, 2\pi, \ldots\) (\(x^2\geq 0\) így a \(-\pi\text{,}\) stb. értékeket nem tekintjük). Összegezve: \(\sin\mathopen{}\left(x^2\right)\mathclose{}=0\) amikor \(x= 0, \pm \sqrt{\pi}, \pm\sqrt{2\pi}, \ldots\text{.}\) Ezen értékekből a \([-2,2]\) intervallumban található a \(0\) és \(\pm\sqrt{\pi}\text{,}\) ahol \(\sqrt{\pi} \approx 1.77\text{.}\)
Újra egy táblázatban adjuk meg a fontos értékeket. Most öt helyen szükséges tekintenünk a függvényt:
\(x= 0, \pm 2, \pm\sqrt{\pi}\text{.}\) Az
\(f\) maximuma a
\([-2,2]\) intervallumon
\(1\text{;}\) a minimuma pedig
\(-1\text{.}\)
Függvényvizsgálat során sokszor nyerhetünk hasznos információkat a következő középérték tételek segítségével.
Tétel 10.1.6. Rolle középérték-tétele.
Legyen \(f\) folytonos az \([a,b]\) intervallumon és differenciálható az \((a,b)\) intervallumon, és \(f(a) = f(b)\text{.}\) Ekkor létezik \(c\) az \((a,b)\) intervallumon, amire \(f'(c) = 0\text{.}\)
Tétel 10.1.7. Lagrange középérték-tétele.
Legyen \(y=f(x)\) folytonos az \([a,b]\) zárt intervallumon és differenciálható az \((a,b)\) nyílt intervallumon. Ekkor létezik olyan \(c\) amire \(a \lt c \lt b\) és
\begin{equation*}
f'(c) = \frac{f(b)-f(a)}{b-a}\text{.}
\end{equation*}
A monotonitás esetében nézzük meg mit tudunk mondani a deriváltak felhasználásával.
Egy szigorúan monoton növekvő
\(f\) függvény esetében, ha
\(b\gt a,\) akkor
\(f(b)\gt f(a),\) azaz ilyen esetekben
\(b-a\gt 0,\quad f(b)-f(a)\gt 0.\) A Lagrange középérték-tétel miatt létezik olyan
\(c\) amire
\(a \lt c \lt b\) és
\begin{equation*}
f'(c) = \frac{f(b)-f(a)}{b-a}\gt 0\text{.}
\end{equation*}
Ami azt mutatja, hogy ahol a függvény szigorú monoton növekvő ott a derivált pozitív.
Tétel 10.1.8. Monotonitás és derivált kapcsolata.
Legyen \(f\) egy folytonos függvény az \([a,b]\) intervallumon és differenciálható az \((a,b)\) intervallumon.
Ha \(f'(c) \gt 0\) minden \(c\) esetén az \((a,b)\)-ből, akkor \(f\) monoton növekvő az \([a,b]\) intervallumon.
Ha \(f'(c) \lt 0\) minden \(c\) esetén az \((a,b)\)-ből, akkor \(f\) monoton csökkenő az \([a,b]\) intervallumon.
Ha \(f'(c) =0\) minden \(c\) esetén az \((a,b)\)-ből, akkor \(f\) konstans az \([a,b]\) intervallumon.
Az előző tételt hogyan is tudjuk alkalmazni a függvényvizsgálat során? Foglaljuk össze milyen stratégiát tudunk követni a deriváltak felhasználásával.
Példa 10.1.10. Monotonitás vizsgálata.
Legyen \(f(x) = x^3+x^2-x+1\text{.}\) Határozzuk meg melyik intervallumokon monoton csökkenő/növekvő az \(f\) függvény!
Megoldás.
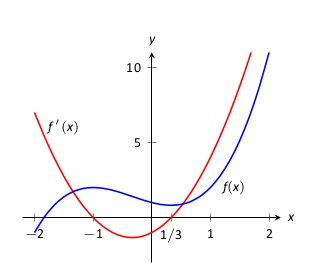
Az \(f\) értelmezési tartománya nincs megadva így a legbővebb halmazt tekintjük, azaz ebben az esetben ez \(\mathbb{R}\) vagy \((-\infty,\infty)\text{.}\) Számítsuk ki \(f\) kritikus értékeit. Kapjuk, hogy \(f'(x) = 3x^2+2x-1 = (3x-1)(x+1)\text{,}\) így \(f'(x) = 0\) akkor teljesül, ha \(x=-1\) vagy \(x=1/3\text{.}\) Továbbá \(f'\) mindig definiált.
Az értelmezési tartományt felosztjuk három részre a két kritikus érték alapján: \((-\infty,-1)\text{,}\) \((-1,1/3)\) és \((1/3,\infty)\text{.}\)
Választunk a részintervallumokból \(p\) értékeket és meghatározzuk \(f'(p)\) előjelét. Csak az előjel érdekel minket, így a választást úgy célszerű megtenni, hogy a számolás lehetőleg a legegyszerűbb legyen.
- 1. részintervallum: \((-\infty,-1)\)
Legyen (tetszőleges választás az intervallumból) \(p=-2\text{.}\) Ekkor \(f'(-2)\text{:}\) \(f'(-2) = 3(-2)^2+2(-2)-1=7\gt 0\text{.}\) Így az \(f\) monoton növekvő a \((-\infty,-1)\) részintervallumon.
- 2. részintervallum: \((-1,1/3)\)
Legyen most \(p=0\text{,}\) ez benne van az intervallumban és könnyű vele számolni. \(f'(0) = -1\lt 0\text{.}\) Ekkor \(f\) monoton csökkenő a \((-1,1/3)\) részintervallumon.
- 3. részintervallum: \((1/3,\infty)\)
Legyen például \(p=1\text{,}\) ekkor \(f'(p) =3(1)^2+2\cdot 1-1 \gt 0\text{.}\) Így az \(f\) monoton növekvő az \((1/3,\infty)\) részintervallumon.
A monoton növekedés és a monoton csökkenés új értelmezése hatékony módszert ad annak meghatározására, hogy egy kritikus pontból maximum, minimum származik vagy éppen egyiknek sem. Képzeljünk el egy függvényt, amely az \(x=c\) kritikus pontig monoton növekszik, majd ezután monoton csökken. Egy gyors vázlat segít megerősíteni, hogy \(f(c)\) lokális maximum. Hasonló állítás tehető lokális minimumokra is.
Tétel 10.1.11. Lokális szélsőérték és derivált kapcsolata.
Legyen \(f\) egy folytonos függvény az \(I\) intervallumon és differenciálható az \(I\)-n, kivéve esetleg az olyan \(c\) helyeket, ahol \(c\) kritikus érték az \(I\) intervallumon.
Ha az \(f'\) előjelet vált a \(c\)-ben pozitívról negatívra, akkor \(f(c)\) lokális maximuma az \(f\)-nek.
Ha az \(f'\) előjelet vált a \(c\)-ben negatívról pozitívra, akkor \(f(c)\) lokális minimuma az \(f\)-nek.
Folytassuk a “szép” függvények vizsgálatát, azaz továbbra is folytonos és differenciálható függvények tulajdonságaira koncentrálunk. Az előző részben bemutattuk, hogyan lehet egy függvény első deriváltját, \(f'\)-t, felhasználni, hogy \(f\)-ről fontos információkat kapjunk. Most ugyanezt a technikát alkalmazzuk magára \(f'\)-re, és megtudjuk, hogy ez mit árul el nekünk \(f\)-ről.
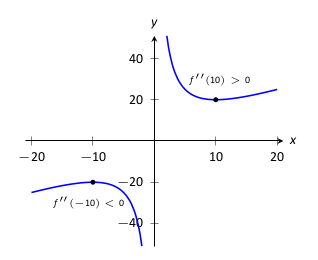
Az \(f'\) tanulmányozásának kulcsa, hogy ennek a függvénynek is tekintjük a deriváltját, nevezetesen \(f''\text{,}\) amely \(f\) második deriváltja. Ha \(f''\gt 0\text{,}\) akkor \(f'\) monoton növekvő. Amikor \(f''\lt 0\text{,}\) \(f' \) monoton csökkenő. Továbbá \(f'\)-nek lokális maximuma/minimuma lehet, amikor \(f''=0\) vagy nem definiált. Nézzük hogyan kaphatunk információt a függvény konvexitásáról a második derivált segítségével.
Tétel 10.1.12. Konvexitás és második derivált.
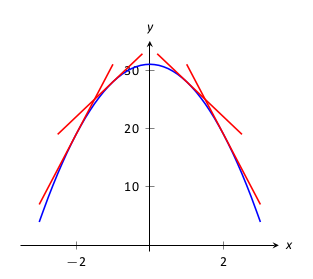
Legyen \(f\) kétszer differenciálható az \(I\) intervallumon. Az \(f\) konvex, ha \(f'' \gt 0\) az \(I\)-n, illetve konkáv, ha \(f''\lt 0\) az \(I\)-n.
Amikor korábban bevezettük függvények tulajdonságait beszéltünk az úgynevezett inflexiós pontokról is, ahol a függvény konvexitása megváltozik. A második deriváltak segítségével ezekről is pontosabb képet kapunk. Ha \(f\) konvexitása megváltozik egy \((c,f(c))\) pontban, akkor \(f' \) növekvőből csökkenőre (vagy csökkenőből növekvőre) vált \(x=c\) esetén. Ez azt jelenti, hogy \(f''\) előjele megváltozik pozitívról negatívra (vagy negatívról pozitívra) az \(x=c\) pontban. Előjelváltás történhet, amikor \(f''=0\) vagy \(f''\) nem definiált. Ez a következő tételhez vezet.
Tétel 10.1.13. Inflexiós pont és második derivált.
Ha \((c,f(c))\) egy inflexiós pont \(f\) grafikonján, akkor vagy \(f''(c)=0\) vagy \(f''\) nincs definiálva \(c\)-nél.
Példa 10.1.14. Konvexitás és inflexiós pontok.
Legyen \(f(x)=x^3-3x+1\text{.}\) Határozzuk meg \(f\) inflexiós pontjait és döntsük el mely intervallumokon konvex/konkáv.
Megoldás.
Ebben az esetben a deriváltak: \(f'(x)=3x^2-3\) és \(f''(x)=6x\text{.}\) Azaz \(f''\) mindig definiált és pontosan akkor 0, ha \(x=0\text{.}\) Az egyetlen inflexiós pontja a görbének: \((0,f(0))=(0,1)\text{.}\)
Az inflexiós pont két részre osztja a számegyenest: \((-\infty,0)\) és \((0,\infty)\text{.}\) Hasonló módon járunk el, mint a monotonitás esetében is, adott intervallumból igyekszünk kiválasztani olyan elemet, amelyre a függvény viszonylag egyszerűen számolható. Itt azt kapjuk, hogy ha \(c\lt 0\text{,}\) akkor \(f''(c)\lt 0\) azaz \(f\) konkáv a \((-\infty,0)\) intervallumon. Egy \(c\gt 0\) választás mellett \(f''(c)\gt 0\) adódik, így \(f\) konvex a \((0,\infty)\) intervallumon.
A függvény első deriváltja egy módszert adott arra, hogy megállapítsuk, vajon egy kritikus érték egy relatív maximumot, minimumot, vagy egyiket sem szolgáltatja a függvénynek. A második derivált egy másik módot kínál arra, hogy teszteljük, vajon egy kritikus pont lokális maximum vagy minimum. A következő tétel megválaszolja, ami intuitív: ha egy kritikus érték olyan területen fordul elő, ahol az \(f\) függvény konvex, akkor annak a kritikus értéknek egy lokális minimumot kell adnia \(f\)-nek.
Tétel 10.1.15. Lokális szélsőértékek és második derivált.
Legyen \(c\) egy kritikus értéke az \(f\)-nek ahol \(f''(c)\) definiált.
Ha \(f''(c)\gt 0\text{,}\) akkor \(f\)-nek lokális minimuma van a \((c,f(c))\) pontban.
Ha \(f''(c)\lt 0\text{,}\) akkor \(f\)-nek lokális maximuma van a \((c,f(c))\) pontban.
Példa 10.1.16. Lokális szélsőérték és derivált.
Legyen \(f(x)=100/x + x\text{.}\) Határozzuk meg \(f\) lokális szélsőértékeit!
Megoldás.
Kiszámítjuk a függvény deriváltjait:
\(f'(x)=-100/x^2+1\) és
\(f''(x) = 200/x^3\text{.}\) Meghatározzuk az
\(f'(x)=0\) megoldásait, hogy megkapjuk a kritikus értékeket (megjegyezzük, hogy
\(f'\) nem definiált
\(x=0\)-ban, de
\(f\) sem, így ez nem lesz kritikus érték.) Kapjuk, hogy
\(x=\pm 10\) a kritikus értékei a függvénynek. Kiértékeljük a második deriváltat. Adódik, hogy
\(f''(10)=0.1\gt 0\text{,}\) azaz lokális minimum van
\(x=10\)-ben. A másik esetben:
\(f''(-10)=-0.1\lt 0\text{,}\) ami lokális maximumot ad
\(x=-10\)-ben.
Példa 10.1.18. Görbe felvázolása.
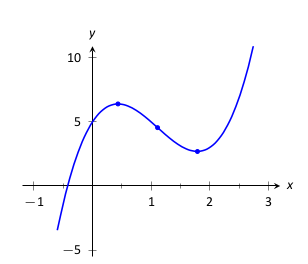
Ebben a példában az \(f(x) = 3x^3-10x^2+7x+5\) függvény grafikonját vázoljuk fel a fent megadott módszert követve.
Megoldás.
A módszerben megadott pontokat követjük.
Az \(f\) értelmezési tartománya a valós számok halmaza, nincsenek problémás helyek a függvény esetében.
Az \(f\) kritikus értékeihez deriválunk. Az első derivált: \(f'(x) = 9x^2-20x+7\text{.}\) Ez egy másodfokú egyenlet, \(f'\) gyökei:
\begin{align*}
x \amp= \frac{20\pm \sqrt{(-20)^2-4(9)(7)}}{2(9)}\\
\amp = \frac19\left(10\pm\sqrt{37}\right)\\
x \amp \approx 0.435, 1.787\text{.}
\end{align*}
Lehetséges inflexiós ponjai az \(f\)-nek: a második derivált \(f''(x) = 18x-20\text{.}\) Ekkor
\begin{align*}
f''(x) \amp = 0\\
18x-20 \amp =0\\
x \amp = 10/9\\
\amp \approx 1.111\text{.}
\end{align*}
Nincsenek függőleges aszimptoták.
A végtelenben vett viselkedést határértékek segítségével kapjuk meg, ahogy \(x\) megközelíti \(\pm \infty \)-t.
\begin{equation*}
\lim_{x\to -\infty} f(x) = -\infty \qquad \lim_{x\to \infty}f(x) = \infty\text{.}
\end{equation*}
Azaz nincsenek vízszintes aszimptotáink.
Az
\(x=(10\pm\sqrt{37})/9\) és
\(x=10/9\) értékeket elhelyezzük egy számegyenesen. Minden részintervallumot monoton növekvőnek vagy monoton csökkenőnek, valamint konvexnek vagy konkávnak jelölünk a korábban alkalmazott technikák segítségével.
-
Meghatározzuk \(f\) értékét minden kritikus helyen és lehetséges inflexiós pontnál.
\begin{align*}
f(0.435)\amp\approx6.400\amp f(1.111)\amp\approx4.547\amp f(1.787)\amp\approx 2.695
\end{align*}
Összekötjük a kapott pontokat figyelve az intervallumokban teljesülő monotonitási és konvexitási tulajdonságaira a függvénynek.