Pont 12.2 Határozott integrál és Riemann-integrál
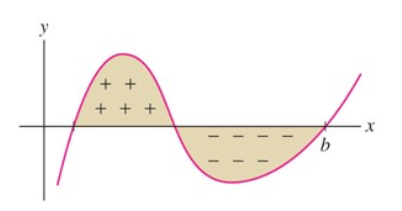
Adott egy függvény grafikonja \(y=f(x)\text{,}\) meg szeretnénk határozni \(y=f(x)\) görbe és az \(x\)-tengely közötti terület nagyságát. Ez a probléma sok gyakorlati kérdésnél felmerül, hogy ezt kezelni tudjuk néhány kifejezést kell definiálnunk.
Definíció 12.2.1. Határozott integrál.
Legyen \(y=f(x)\) egy \([a,b]\) zárt intervallumon definiált függvény. Az \(f\) előjeles területe az \(x=a\)-tól \(x=b\)-ig:
(az \(y=f(x)\) görbe alatti és az \(x\)-tengely feletti terület az \([a,b]\) intervallumon) \(-\) (az \(y=f(x)\) görbe feletti és az \(x\)-tengely alatti terület az \([a,b]\) intervallumon).
Az \(f\) függvény határozott integrálja az \([a,b]\) intervallumon az \(f\) előjeles területe az \([a,b]\)-n, jelölés:
\begin{equation*}
\int_a^b f(x)\, dx\text{,}
\end{equation*}
ahol \(a\) és \(b\) az integrálás határai.
Egy olyan példával kezdünk, ahol a terület számítása a geometriából jól ismert háromszögekre vonatkozó formulával meghatározható egyszerűen.
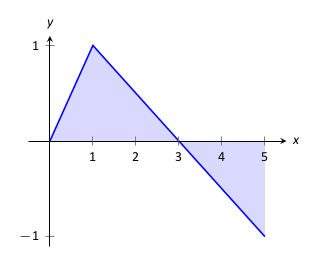
Legyen az
\(y=f(x)\) függvényünk a következő grafikonnal megadva:
Számítsuk ki az alábbi határozott integrálokat:
\(\displaystyle \int_0^3 f(x)\, dx\)
\(\displaystyle \int_3^5 f(x)\, dx\)
\(\displaystyle \int_0^5 f(x)\, dx\)
\(\displaystyle \int_0^3 5f(x)\, dx\)
\(\displaystyle \int_1^1 f(x) \, dx\)
\(\int_0^3 f(x)\, dx\) az \(f\) alatti terület a \([0,3]\) intervallumon. Ez egy háromszög területével egyenlő: azaz \(\int_0^3 f(x)\, dx=\frac12(3)(1) = 1.5\text{.}\)
\(\int_3^5 f(x)\, dx\) nem más, mint az \(x\)-tengely alatti terület a \([3,5]\) intervallumon. Ez a terület ismét egy háromszög területe: \(\frac12(2)(1) = 1\text{;}\) ez az \(x\)-tengely alatt van, ezért \(\int_3^5 f(x)\, dx = -1\text{.}\)
\(\int_0^5f(x)\, dx\text{:}\) ez itt a teljes előjeles területe \(f\)-nek a \([0,5]\) intervallumon. Az előbbiek alapján: \(1.5 + (-1) = 0.5\text{.}\)
\(\int_0^35f(x)\, dx\text{:}\) ez az \(5f\) függvény alatti terület a \([0,3]\) intervallumon. Ez is egy háromszög területe: \(\int_0^35f(x)\, dx = \frac12(15)(1) = 7.5\text{.}\)
\(\int_1^1f(x)\, dx\text{:}\) ebben az esetben az \(f\) területe az \([1,1]\) “intervallumon” a keresett érték, de ez 0.
Tétel 12.2.2. Határozott integrál tulajdonságai.
Legyenek \(f\) és \(g\) az \(I\) zárt intervallumon definiált függvények és \(a\text{,}\) \(b\) és \(c\) az \(I\) elemei, továbbá \(k\) egy konstans. Ekkor az alábbi tulajdonságok teljesülnek:
\(\displaystyle \int_a^a f(x)\, dx = 0\)
\(\displaystyle \int_a^b f(x)\, dx + \int_b^c f(x)\, dx = \int_a^cf(x)\, dx\)
\(\displaystyle \int_a^bf(x)\, dx = -\int_b^a f(x)\, dx\)
\(\displaystyle \int_a^b\big(f(x)\pm g(x)\big)\, dx = \int_a^bf(x)\, dx \pm \int_a^bg(x)\, dx\)
\(\displaystyle \int_a^bk\cdot f(x)\, dx = k\cdot\int_a^bf(x)\, dx\)
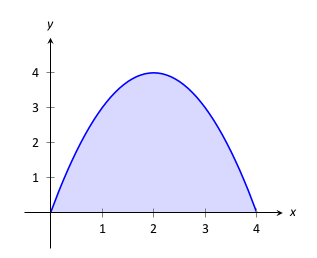
A korábbi példában a függvényünk megfelelően egyszerű volt abból a szempontból, hogy a területek számítása háromszögek területének kiszámítására volt visszavezethető. Ez természetesen nem fog működni általában. Egy alapvető számítási technika az, hogy először egy adott problémát egy közelítéssel válaszolunk meg, majd ezt a közelítést finomítjuk, hogy jobbá tegyük, végül pedig határértékeket alkalmazunk a finomítási folyamat során az pontos válasz meghatározására. Ezt fogjuk követni itt is. Legyen most a függvényünk
\(y=f(x)=4x-x^2.\) Hogyan határozzuk meg
\begin{equation*}
\int_0^4 (4x-x^2) dx
\end{equation*}
értékét? Ezt téglalapok segítségével fogjuk közelíteni.
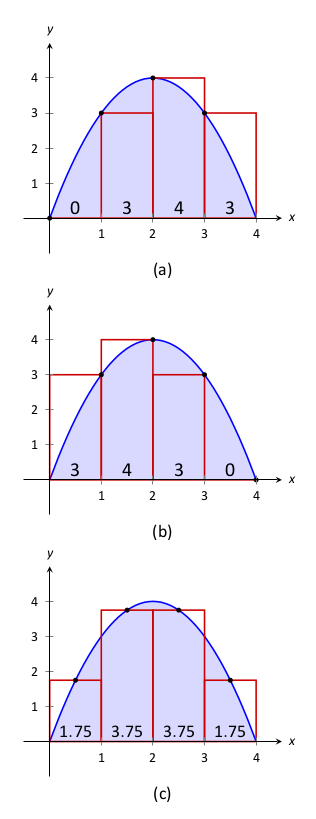
Az ábrán három különböző beosztáshoz tartozó közelítést figyelhetünk meg, az a) és b) esetekben a téglalapok területei összesen 10 egységnyiek, a c) esetben pedig 11. A beosztás finomítása egy természetes ötlet a pontosabb eredmény eléréséhez.
Definíció 12.2.3. Beosztás.
Egy \(\Delta x\) besztása az \([a,b]\) zárt intervallumnak: \(x_0\text{,}\) \(x_1\text{,}\) \(\ldots\) \(x_{n}\) ahol
\begin{equation*}
a=x_0 \lt x_1 \lt \ldots \lt x_{n-1} \lt x_{n}=b\text{.}
\end{equation*}
Az \(i\)-ik részintervallum \([x_{i-1},x_{i}]\) hossza: \(\Delta x_i = x_{i}-x_{i-1}\text{.}\) Ha az \([a,b]\) intervallumot egyenlő részekre osztjuk, akkor \(\Delta x\) jelöli egy adott részintervallum hosszát.
A beosztások segítségével fel tudjuk írni a téglalapok területeit és ezeket összegezni tudjuk.
Definíció 12.2.4. Riemann-összegek.
Legyen \(f\) egy zárt \([a,b]\) intervallumon definiált függvény, továbbá legyen \(\Delta x\) az \([a,b]\) egy beosztása, \(c_i\) jelöljön egy tetszőleges elemet az \(i\)-ik részintervallumból.
Az alábbi típusú összeget az \(f\) függvény \([a,b]\) intervallumra vonatkozó Riemann-összegének nevezzük:
\begin{equation*}
\sum_{i=1}^n f(c_i)\Delta x_i.
\end{equation*}
Tekintsük újra a korábbi példánkat: \(\int_0^4(4x-x^2)\, dx\text{.}\) Osszuk fel \(n\) egyenlő részre a \([0,4]\) intervallumot. Ekkor \(\Delta x = \frac{4-0}{n} = 4/n\) és \(x_i = 0 + i\Delta x = 4i/n\text{.}\) Jöhetnek a megfelelő téglalapok területei, azaz egy Riemann-összeg:
\begin{align*}
\int_0^4(4x-x^2)\, dx \amp \approx \sum_{i=1}^n f(x_{i})\Delta x\\
\amp = \sum_{i=1}^n f\left(\frac{4i}{n}\right) \Delta x\\
\amp = \sum_{i=1}^n \left[4\frac{4i}n-\left(\frac{4i}n\right)^2\right]\Delta x\\
\amp = \sum_{i=1}^n \left(\frac{16\Delta x}{n}\right)i - \sum_{i=1}^n \left(\frac{16\Delta x}{n^2}\right)i^2\\
\amp = \left(\frac{16\Delta x}{n}\right)\sum_{i=1}^n i - \left(\frac{16\Delta x}{n^2}\right)\sum_{i=1}^n i^2\\
\amp = \left(\frac{16\Delta x}{n}\right)\cdot \frac{n(n+1)}{2} - \left(\frac{16\Delta x}{n^2}\right)\frac{n(n+1)(2n+1)}{6}\\
\amp =\frac{32(n+1)}{n} - \frac{32(n+1)(2n+1)}{3n^2} (\text{ emlékezzünk rá, hogy } \Delta x = 4/n)\\
\amp = \frac{32}{3}\left(1-\frac{1}{n^2}\right) \text{ (egyszerűsítés után). }
\end{align*}
Ahogyan finomítjuk a beosztásokat, az eredmény egyre pontosabb lesz, jöhet a határérték!
\begin{align*}
\int_0^4 (4x-x^2)\, dx \amp = \lim_{n\rightarrow \infty} \frac{32}{3}\left(1-\frac{1}{n^2}\right)\\
\amp = \frac{32}{3}\left(1-0\right)\\
\amp = \frac{32}{3}.
\end{align*}
Most bevezetünk három adott beosztáshoz tartozó Riemann-összeget, amelyeknél a téglalapok területei viszonylag egyszerűen számolhatóak konkrét esetekben:
\(\displaystyle S_B(n) = \sum_{i=1}^n f(x_{i-1})\Delta x\text{,}\)
\(\displaystyle S_J(n) = \sum_{i=1}^n f(x_{i})\Delta x\text{,}\)
\(\displaystyle S_K(n) = \sum_{i=1}^n f\left(\frac{x_{i-1}+x_{i}}{2}\right)\Delta x\text{.}\)
Tétel 12.2.5. Riemann-összegek határértékei.
Legyen \(f\) egy folytonos függvény az \([a,b]\) zárt intervallumon és \(S_B(n)\text{,}\) \(S_J(n)\text{,}\) \(S_K(n)\text{,}\) \(\Delta x\text{,}\) \(\Delta x_i\) és \(c_i\) a korábban definiáltak szerint. Ekkor teljesülnek az alábbiak:
\(\displaystyle \displaystyle \lim_{n\to\infty} S_B(n) = \lim_{n\to\infty} S_J(n)
= \lim_{n\to\infty} S_K(n)
= \lim_{n\to\infty}\sum_{i=1}^n f(c_i)\Delta x\)
\(\displaystyle \displaystyle \lim_{n\to\infty}\sum_{i=1}^n f(c_i)\Delta x = \int_a^b f(x)\, dx.\)