Pont 13.1 Határozott integrál és alkalmazásai
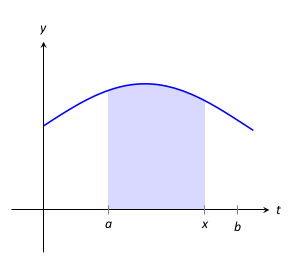
Legyen \(f(t)\) egy folytonos függvény, amely az \([a,b]\) intervallumon van definiálva. Az \(\int_a^b f(x)\, dx\) határozott integrál az “f alatt lévő terület” az \([a,b]\) intervallumon, ahogyan ezt a korábbi fejezetben láttuk. Ezt a fogalmat függvénnyé alakíthatjuk azáltal, hogy a felső (vagy alsó) határt változtatjuk.
Legyen
\(F(x) = \int_a^x f(t)\, dt\text{.}\) Ez a függvény kiszámítja az
\(f\) alatti területet az
\([a,x]\) intervallumon, ahogy azt az ábra mutatja.
Ezt a függvényt a határozott integrál ismereteink felhasználásával tanulmányozhatjuk. Például,
\(F(a)=0\text{,}\) mivel
\(\int_a^af(t)\, dt=0\text{.}\)
Tétel 13.1.1. Határozott integrál - alaptétel.
Legyen \(f\) folytonos az \([a,b]\) intervallumon és legyen \(F(x) = \int_a^x f(t)\, dt\text{.}\) Ekkor \(F\) folytonos az \([a,b]\) intervallumon, differenciálható az \((a,b)\) intervallumon és
\begin{equation*}
F'(x)=f(x)\text{.}
\end{equation*}
Vegyünk egy \(f\) függvényt, amely egy \(a\text{,}\) \(b\) és \(c\) értékeket tartalmazó nyílt intervallumon van definiálva. Tegyük fel, hogy ki akarjuk számítani \(\int_a^b f(t)\, dt\) értékét. Először legyen
\begin{equation*}
F(x) = \int_c^x f(t)\, dt\text{.}
\end{equation*}
A határozott integrál tulajdonságait felhasználva tudjuk, hogy
\begin{align*}
\int_a^b f(t)\, dt \amp = \int_a^c f(t)\, dt + \int_c^b f(t)\, dt\\
\amp = -\int_c^a f(t)\, dt + \int_c^b f(t)\, dt
\end{align*}
Legyen \(x=a\) az első integrálban és \(x=b\) a második integrálban, így \(\int_c^a f(t)\, dt =F(a)\) és \(\int_c^b f(t)\, dt =F(b)\text{.}\) Ezért:
\begin{align*}
\int_a^b f(t)\, dt \amp =-F(a) + F(b)\\
\amp = F(b) - F(a)\text{.}
\end{align*}
Most láthatjuk, hogyan kapcsolódnak egymáshoz az határozatlan integrálok és a határozott integrálok: egy határozott integrált a primitív függvények segítségével ki tudunk értékelni.
Tétel 13.1.2. Newton-Leibniz-formula.
Legyen \(f\) folytonos az \([a,b]\) intervallumon és legyen \(F\) bármely primitív függvénye \(f\)-nek. Ekkor
\begin{equation*}
\int_a^b f(x)\, dx = F(b) - F(a)\text{.}
\end{equation*}
Példa 13.1.3. Newton-Leibniz formula - alkalmazás.
Vizsgáltuk numerikusan és határértéket felhasználva az \(\int_0^4(4x-x^2)\ dx\) kifejezést. Nézzük meg hogyan kezelhetjük ezt a Newton-Leibniz formula segítségével.
Megoldás.
Szükségünk van az \(f(x)=4x-x^2\) függvény egy primitív függvényére. Az \(f\) összes primitív függvénye a következő formában áll elő: \(F(x) = 2x^2-\frac13x^3+C\text{;}\) az egyszerűség kedvéért válasszuk \(C=0\)-t.
A Newton-Leibniz formula a következőre vezet:
\begin{equation*}
\int_0^4(4x-x^2)\ dx = F(4)-F(0) = \big(2(4)^2-\frac134^3\big)-\big(0-0\big) = 32-\frac{64}3 = 32/3\text{.}
\end{equation*}
Ez ugyanaz a válasz, amelyet a korábbi fejezetben határértékek alkalmazásával kaptunk, csak sokkal kevesebb munkával.
Alpont 13.1.1 Görbék által határolt terület
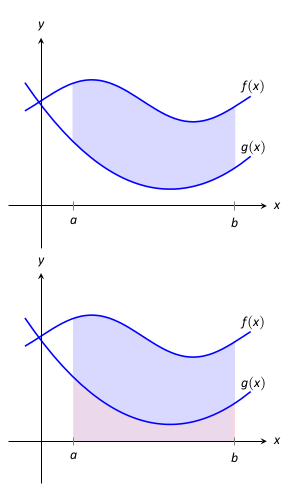
Tekintsük az
\(f(x)\) és
\(g(x)\) folytonos függvényeket, amelyek az
\([a,b]\) intervallumon vannak definiálva, ahol
\(f(x) \geq g(x)\) minden
\(x\) esetén az
\([a,b]\) intervallumon, ahogyan azt az alábbi ábra is szemlélteti.
Mi a területe a két görbe által határolt régiónak az
\([a,b]\) intervallumon? Ez a terület “az
\(f\) alatti terület
\(-\) a
\(g\) alatti terület.” Matematikai jelöléssel ez nem más, mint:
\begin{equation*}
\int_a^b f(x)\ dx - \int_a^b g(x)\ dx\text{.}
\end{equation*}
A határozott integrál tulajdonságai lehetővé teszik számunkra, hogy ezt a kifejezést egyszerűsítsük:
\begin{equation*}
\int_a^b\big(f(x) - g(x)\big)\ dx\text{.}
\end{equation*}
Tétel 13.1.4. Görbék által határolt terület.
Legyenek \(f(x)\) és \(g(x)\) folytonos függvények, amelyek az \([a,b]\) intervallumon vannak definiálva, ahol \(f(x)\geq g(x)\) minden \(x\) esetén az \([a,b]\) intervallumban. Az \(y=f(x)\text{,}\) \(y=g(x)\) görbék, valamint az \(x=a\) és \(x=b\) egyenesek által határolt terület a következőképpen számítható ki:
\begin{equation*}
\int_a^b \big(f(x)-g(x)\big)\ dx\text{.}
\end{equation*}
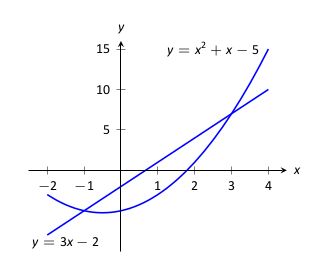
Példa 13.1.5. Terület meghatározás.
Határozzuk meg az
\(y=x^2+x-5\) és
\(y=3x-2\) görbék által meghatározott terület nagyságát.
Megoldás.
A két görbe metszi egymást, a metszéspontokat kiszámolhatjuk ebben az esetben, hiszen másodfokú polinomok gyökeinek meghatározására redukálódik a probléma:
\begin{align*}
x^2+x-5 \amp = 3x-2\\
(x^2+x-5) - (3x-2) \amp = 0\\
x^2-2x-3 \amp = 0\\
(x-3)(x+1) \amp = 0\\
x\amp =-1,\ 3\text{.}
\end{align*}
A tétel alapján most már intergrálással ki tudjuk számítani a területet:
\begin{align*}
\int_{-1}^3\big(3x-2 -(x^2+x-5)\big)\ dx \amp = \int_{-1}^3 (-x^2+2x+3)\ dx\\
\amp =\left.\left(-\frac13x^3+x^2+3x\right)\right|_{-1}^3\\
\amp =-\frac13(27)+9+9-\left(\frac13+1-3\right)\\
\amp = 10\frac23 = 10.\overline{6}
\end{align*}
Alpont 13.1.2 Forgástestek térfogata
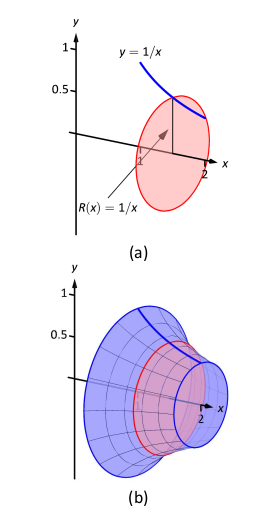
Kezdjük egy \(y = f(x)\) függvénnyel az \(x = a\) és \(x = b\) között. Ennek a görbének a vízszintes tengely körüli forgatása egy háromdimenziós szilárd testet hoz létre, amelynek metszetei korongok (vékony körök). Legyen \(R(x)\) a keresztszelvény korongjának sugara \(x\)-nél; ennek a korongnak a területe \(\pi R(x)^2.\) Ekkor a következő eredményre jutunk.
Tétel 13.1.6. Forgástestek térfogata.
Tekintsünk egy szilárd testet, amelyet az \(y = f(x)\) görbe \(x = a\)-tól \(x = b\)-ig a vízszintes tengely körül való forgatással képezünk. Legyen \(R(x)\) a keresztmetszeti kör sugara \(x\)-nél. A szilárd test térfogata:
\begin{equation*}
V =\pi \int_a^b R(x)^2\ dx\text{.}
\end{equation*}
Példa 13.1.7. Forgástest térfogata.
Határozzuk meg annak a szilárd testnek a térfogatát, amely az
\(y=1/x\) görbe
\(x=1\)-től
\(x=2\)-ig terjedő
\(x\)-tengely körüli forgatásával áll elő.
Megoldás.
Alkalmazzuk a fenti tételt:
\begin{align*}
V \amp = \pi\int_1^2 \frac1{x^2}\, dx\\
\amp = \pi\int_1^2 \left(\frac1x\right)^2\, dx
\end{align*}
\begin{align*}
\amp = \pi\left[-\frac1x\right]\Big|_1^2\\
\amp = \pi \left[-\frac12 - \left(-1\right)\right]\\
\amp = \frac{\pi}{2}\text{.}
\end{align*}