Alkalmazások

Pont 11.1 Alkalmazások

Alpont 11.1.1 Newton módszer

A függvényelemzésnél láttuk, hogy az első- és második derivált zérushelyei fontos szerepet töltenek be. Konkrét példák esetében a megoldások explicit meghatározása nem mindig egyszerű feladat. Meg tudunk oldani lineáris egyenleteket, másodfokú egyenleteket, a harmad- és negyedfokú polinomokra is létezik eljárás, bizonyos trigonometrikus és exponenciális egyenleteket is tudunk kezelni. Nagyon sok esetben ez már nem így van, ilyenkor megpróbálhatunk valamilyen közelítő módszert alkalmazni.

Newton módszere érintőket használ. A fő ötlet az, hogy ha \(x\) elég közel van az \(f(x)\) egy gyökéhez, akkor a gráf \((x,f(x))\) pontján áthaladó érintő az \(x\)-tengelyt egy olyan pontban metszi, amely közelebb van a gyökhöz, mint \(x\text{.}\)

Newton módszerét egy gyöktől nem túl messze elhelyezkedő, de tetszőleges pontból indítjuk. Ezt nevezzük \(x_0\)-nak. Rajzoljuk meg a tangens egyenest a grafikonon az \((x_0,f(x_0))\) pontban, és nézzük meg, hol metszi az \(x\)-tengelyt. Ezt a pontot nevezzük \(x_1\)-nek. Ezután ismételjük meg a folyamatot: rajzoljuk meg a tangens egyenest a grafikonon az \((x_1, f(x_1))\) pontban, és nézzük meg, hol metszi az \(x\)-tengelyt. Ezt a pontot nevezzük \(x_2\)-nek. Ismételjük meg az eljárást, hogy megkapjuk \(x_3\)-at, \(x_4\)-et stb. Ez a pontsorozat gyakran meglehetősen gyorsan konvergál az \(f\) gyökéhez.

Ezt a geometriai eljárást felhasználhatjuk egy algebrai módszer létrehozására. Nézzük meg, hogyan találtuk meg \(x_1\)-et. A grafikon érintőjével kezdtünk az \((x_0,f(x_0))\) pontban. Ennek az érintőnek a meredeksége \(f'(x_0)\text{,}\) és az egyenes egyenlete

\begin{equation*} y=f'(x_0)(x-x_0)+f(x_0)\text{.} \end{equation*}

Ez az egyenes akkor metszi az \(x\) tengelyt, amikor \(y=0\text{.}\) Az \(x\) érték, ahol metszi, azt \(x_1\)-nek nevezzük. Így a következő egyenlethez jutunk:

\begin{equation*} 0 = f'(x_0)(x_1-x_0)+f(x_0)\text{.} \end{equation*}

Innen kapjuk, hogy

\begin{equation*} x_1=x_0-\frac{f(x_0)}{f'(x_0)}\text{.} \end{equation*}

Általánosságban, adott egy közelítés \(x_n\text{,}\) megtalálhatjuk a következő approximációt \(x_{n+1}\)-et a következőképpen:

\begin{equation*} x_{n+1} = x_{n} - \frac{f(x_{n})}{f'(x_{n})}\text{.} \end{equation*}

Módszer 11.1.1. Newton módszer.

Legyen \(f\) egy differenciálható függvény egy \(I\) intervallumon, amelynek van gyöke \(I\)-ben. A gyök értékének megközelítése \(d\) tizedesjegy pontossággal a következő módon történhet.

Válassztunk egy \(x_0\) értéket a gyök közelítő kezdeti értékeként. (Ez gyakran az \(f\) grafikonjának segítségével történik.)
A közelítéseket iterálással számoljuk: adott egy közelítés \(x_n\text{,}\) kiszámítjuk a következő közelítést \(x_{n+1}\)-et:

\begin{equation*} x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}\text{.} \end{equation*}
Az iterációt addig végezzük amíg az új approximált érték az első \(d\) tizedeshelyen nem egyezik az előzővel.

Alpont 11.1.2 Bevétel-költség-profit

A lineáris modelleknél bevezettük a bevétel-, költség- és profit függvényeket. Vizsgáltuk a hozzájuk kapcsolódó grafikonok metszéspontjait és már ezek felhasználásával meg tudtunk válaszolni egyszerű kérdéseket. Most már a függvényvizsgálat eszköztára is rendelkezésünkre áll, így érdemes visszatérni erre a kérdéskörre. Megvizsgáljuk a "profit maximalizálása" és a "bevétel maximalizálása", illetve a "költségek minimalizálása" közötti különbségeket. Elképzelünk egy eladót, akinek fagylaltos kocsija van a Central Park forgalmas kereszteződésében. A fagylaltárus megfigyeli, hogy ha fagylaltonként 3 dollárt kér el tölcsérért, naponta csak 120 tölcsért ad el. Másrészt, ha 2 dollárt kér egy fagylaltkehelyért, akkor 200 fagylaltkehelyet ad el naponta. Példánkban, mivel már régen kifizette az indulási költségeit, az üzleti tevékenység költségei csak 50 cent/tölcsér, plusz napi 100 dollár az eladási engedélyért fizetendő díj a Central Parkban. Megfigyelhetjük, hogy ha túl magas árat szab, akkor túl kevés tölcsért ad el, és nem sok hasznot fog termelni; ha az árat úgy alakítja ki, hogy túl alacsony, akkor több tölcsért fog eladni, de még így sem fog sok hasznot termelni. Többféleképpen is megmutatható, hogy a kereslet \(n\text{,}\) és az ár \(p\text{,}\) a következő összefüggést fogja mutatni

\begin{equation*} n=360-80p \end{equation*}

vagy

\begin{equation*} p=4.5-\frac{n}{80}. \end{equation*}

Álljunk meg egy pillanatra, és nézzük meg, van-e ennek értelme. Először is, az \(n = 200\) és \(n = 120\) esetekben megkapjuk a várt 2 és 3 dolláros árakat. Ha \(p = 2.5\)-et állítunk be, akkor 160-at kapunk, ahogyan azt vártuk - ez a középpont. Az egyenletek megtalálásának egyszerű módja az, hogy kiszámítjuk a meredekséget. A \((200,2)\) és \((120,3)\) pontokat összekötő egyenes meredekségének kiszámítása, majd az egyenes egyenletének kiszámítása a két pont között. A modell tehát a

\begin{equation*} 0\leq p\leq 4.50 \end{equation*}

esetében érvényes vagy ennek megfelelően

\begin{equation*} 0\leq n\leq 360. \end{equation*}

Most szeretnénk bevételi, költség- és profitfüggvényt készíteni az eladott tölcsérek számának, \(n\)-nek a függvényében. A bevételi függvény:

\begin{equation*} r(n)=np=4.5n-\frac{n^2}{80}, \end{equation*}

a költség függvény:

\begin{equation*} c(n)=0.5n+100, \end{equation*}

a profit függvény:

\begin{equation*} p(n)=\frac{-n^2}{80}+4n-100. \end{equation*}

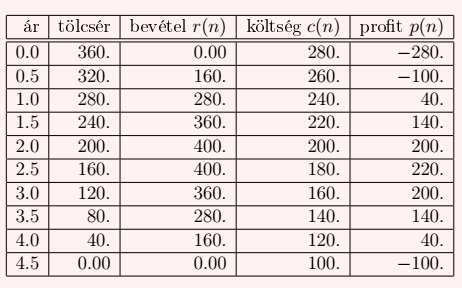
Néhány helyen számoljuk ki a függvények értékét:

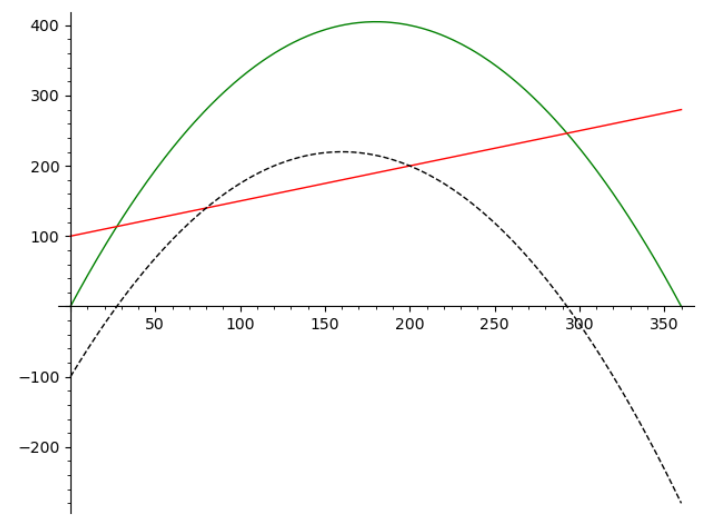
Ábrázoljuk ezeket a függvényeket.

Az ábrán a zöld függvény a bevétel, itt lokális maximumot találhatunk, ahol a derivált eltűnik, \(r'(n)=-\frac{1}{40}n+4.5\text{,}\) aminek a zérushelye: 180. Az ábrán a fekete görbe tartozik a profithoz, itt a derivált: \(p'(n)=-\frac{1}{40}n+4\text{,}\) aminek a zérushelye: 160.

El.Top Köv.