2013 június

Az Erdős-Graham probléma

2013. június 20.

Számtani sorozatok és algebrai görbék pontjai

2013. június 21.

2013 július

Sage matematikai programcsomag

2013. július 24.

Az alábbiakban bemutatjuk a kutatás során használt Sage matematikai programcsomagot. Ez egy ingyenesen elérhető, komoly tudással rendelkező szoftver, amelyet lehet használni algebra, analízis, gráfelmélet, kombinatorika, számelmélet területeken.
Először az Erdős-Graham probléma esetében mutatunk be egy eljárást, melynek segítségével a kapcsolódó egyenletet lehet vizsgálni olyan esetekben, amikor a két blokk távolsága rögzített. Két négy hosszú blokk szorzatát vizsgáljuk, mikor lehet négyzetszám, azaz a következő diofantikus egyenletet: \[ x(x+1)(x+2)(x+3)(x+k)(x+k+1)(x+k+2)(x+k+3)=y^2. \] Ezt átírjuk a következő alakban: \[ x(x+k+3)(x+1)(x+k+2)(x+2)(x+k+1)(x+3)(x+k)=y^2. \] Így a polinomot egyszerűbb alakra tudjuk hozni: \[ X(X+k+2)(X+2k+2)(X+3k)=y^2, \] ahol \(X=x^2+(k+3)x\).

A fenti numerikus számolások alapján pl. \(k=12\) esetében kapjuk, hogy \(X\in [0,13,28]\) megoldáshoz vezet. Azaz \[ \begin{aligned} 0 & =x^2+(12+3)x\\ 13 & =x^2+(12+3)x\\ 28 & =x^2+(12+3)x. \end{aligned} \] Másodfokú egyenletek megoldása egyszerű, most bízzuk ezt is a Sage-re:

Az előző számolások alapján csak két egész megoldás van \(0\) és \(-15\), de mi csak pozitív megoldásokat keresünk.

2013 augusztus

Erdős Centennial

2013. augusztus 22.

Az idei évben rendezték meg Budapesten az Erdős Centennial konferenciát július 1 és 5 között. A világ minden tájáról érkeztek matematikusok. A nagyon jól szervezett konferenciának a Magyar Tudományos Akadémia épülete adott otthont. A konferencia honlapjáról: Erdős Centennial sok érdekességet tudhatunk meg Erdős Pál életéről, munkásságáról. Több érdekes előadás is volt a kutatási témámhoz kötődően. Kiemelném a Diophantine Number Theory szekciót, amelyben 6 előadás hangzott el. Az egyik előadást Győry Kálmán professzor tartotta Perfect powers in products with terms from arithmetic progression - A survey címmel. Ebben az Erdős-Selfride eredmény általánosításairól volt szó, azaz igen szorosan kapcsolódik az Erdős-Graham problémához.

2013 szeptember

21st Czech and Slovak International Conference on Number Theory

2013. szeptember 27.

Szeptember 2 és 6 között került megrendezésre a "21st Czech and Slovak International Conference on Number Theory" konferencia Ostraviceben. Ez egy nagy hagyományokra visszatekintő 2 évente megrendezésre kerülő számelméleti konferencia. A legtöbb előadó a régióból érkezik, de mindig akad egy-egy egzotikusabb országból származó matematikus is. Számomra azért is kedves ez a sorozat, mert 1999-ben az első nemzetközi konferencia előadásomat éppen ennek keretében tartottam. Most is beszéltem friss kutatási eredményekről, amelyek már a Magyary Ösztöndíjhoz kötődnek.

Kutatók Éjszakája

2013. szeptember 28.

Szeptember 27-én országszerte sok érdekes, izgalmas előadás került megrendezésre a Kutatók Éjszakája keretében. Debrecenben a Matematikai Intézetben is színes volt a program. Nagy örömmel töltött el, hogy az M426-os termet sikerült úgy megtölteni még a pótszékek sem bizonyultak elegendőnek. Egy kártyatrükk matematikai hátterét mutattuk meg az érdeklődőknek. Külön öröm volt számomra, hogy egykori egyetemi évfolyamtársammal Bessenyei Mihállyal háromszor is sikeresen végrehajtottuk a trükköt. Az alábbiakban mellékelem az előadás anyagát. A trükk működését a Sage programcsomagban is bemutattuk, amit az alábbiakban ki lehet próbálni. Arra kell figyelni, hogy egy adott lap alapértelmezett értékét átírva ne legyen az öt lap között két azonos a segéd rendezése résznél, és a négy lap között a bűvész megfejtése résznél.

2013 október

Elliptikus görbék

2013. október 28.

A kutatási témánk egyik része algebrai görbékhez kapcsolódik. A problémakör bemutatatásához elliptikus görbéket fogunk használni. Elliptikus görbéket több alakban is meg lehet adni, most mi az \[E:\quad y^2=x^2+ax+b\] formát tekintjük. Egy ilyen görbét lehet vizsgálni különböző struktúrák felett: véges testek, racionális számok teste, valós számok teste, komplex számok teste. Bevezetjük a következő jelölést: \[E(\mathbb{Q})=\{(x,y):\quad x,y\in\mathbb{Q}, y^2=x^3+ax+b\}.\] Azaz \(E(\mathbb{Q})\) a görbén található racinális pontok halmaza. Mitől lesz algebrai a görbe? Most már adott egy halmaz, ha a halmazon értelmezünk egy műveletet, akkor szerencsés esetben valamilyen algebrai struktúrát kapunk. Ezt meg is lehet tenni. Megadható egy összeadás a pontok között. Az elliptikus görbékről és az összeadásról a következő oldalon találunk részletesebb ismertetőt. Elliptikus görbék.
Az alábbiakban bemutatjuk az összeadást egy konkrét görbén adott pontokra nézve. A görbe alakja itt \[y^2=x^3-3x+7.\]

2013 november

Az Erdős-Graham probléma egy általánosítása

2013. november 26.

Varga Nórával közösen vizsgáltuk az Erdős-Graham probléma egy általánosítását. Tekintettük az \[\frac{x(x+1)(x+2)(x+3)}{(x+a)(x+b)}=y^2\] egyenletet. Ebben az esetben sikerült olyan felső korlátot nyerni a megoldásokra Runge-módszert felhasználva, amit konkrét egyenletek esetében fel lehet használni az összes egész megoldás meghatározására. A cikket közlésre elfogadták, 2014 első felében fog megjelenni.

2013 december

Az Erdős-Graham probléma egy általánosítása II.

2013. december 21.

Varga Nórával folytattuk az Erdős-Graham probléma egy általánosításának a vizsgálatát. Tekintettük az \[\frac{x(x+1)(x+2)(x+3)(x+4)(x+5)}{(x+a)(x+b)}=y^2,\] \[\frac{x(x+1)(x+2)(x+3)(x+4)(x+5)}{(x+a)(x+b)(x+c)}=y^3,\] \[\frac{x(x+1)(x+2)(x+3)(x+4)(x+5)}{(x+a)(x+b)(x+c)(x+d)}=y^2\] egyenleteket. Az első és harmadik egyenlet esetében a problémát vissza lehet vezetni hiperelliptikus egyenletek egész megoldásainak meghatározására. Ekkor a következő két egyenlet adódik: \[x(x+1)(x+2)(x+3)(x+4)(x+5)(x+a)(x+b)=U^2,\] \[x(x+1)(x+2)(x+3)(x+4)(x+5)(x+a)(x+b)(x+c)(x+d)=V^2.\] Ezeket Baker-módszer segítségével is lehet vizsgálni, azonban az ott adódó korlátok túl nagyok. Egy másik lehetőség Chabauty-módszerének alkalmazása, de ebben az esetben génusz hármas és négyes görbe Mordell-Weil csoportjának a rangját és generátorait kellene meghatározni. Runge-módszer segítségével viszont gyakorlatban is használható korlátokat sikerült nyerni. A második egyenlet esetében nem is igazán látszik hogyan lehetne más úton kezelni a kérdést.

2014 január

Az \(\frac{x(x+1)(x+2)(x+3)(x+4)(x+5)}{(x+a)(x+b)(x+c)}=y^3\) diofantikus egyenlet

2014. január 28.

Tekintjük az \[\frac{x(x+1)(x+2)(x+3)(x+4)(x+5)}{(x+a)(x+b)(x+c)}=y^3,\] diofantikus egyenletet, ahol \(a,b,c\) különböző egészek úgy, hogy \(a,b,c\notin\{0,1,2,3,4,5\}\). Runge-módszer segítségével meg lehet mutatni, hogy ha létezik nagy megoldás, akkor \[y=x+5-\frac{a+b+c}{3}\]. A kis megoldásokra pedig bizonyos polinom egyenletek biztosítanak korlátot. Az alábbiakban az elméleti eredmény alapján elkészült Sage kódot mutatjuk be, amely adott \(a,b,c\) esetén meghatározza az egyenlet összes egész \((x,y)\in\mathbb{Z}^2\) megoldását.

2014 február

Rational Function Variant of a problem of Erdős-Graham Problem

2014. február 17.

Közlésre benyújtottuk a Varga Nórával közösen készített cikkünket. A publikációban vizsgáltuk a \[\frac{x(x+1)(x+2)(x+3)(x+4)(x+5)}{(x+a)(x+b)}=y^2,\] \[\frac{x(x+1)(x+2)(x+3)(x+4)(x+5)}{(x+a)(x+b)(x+c)}=y^3,\] \[\frac{x(x+1)(x+2)(x+3)(x+4)(x+5)}{(x+a)(x+b)(x+c)(x+d)}=y^2\] diofantikus egyenleteket. Igazoltuk, hogy ha létezik "nagy megoldás", akkor az osztója egy pozitív egésznek, ami csak a paraméterektől függ. A "kis megoldásokra" pedig sikerült a gyakorlatban is használható korlátot adni. Ezen felül az elméleti eredményeket felhasználva algoritmust adtunk konkrét egyenletek összes egész megoldásának meghatározására és ezt a Sage programcsomagban implementáltuk is.

2014 március

Számtani sorozatok negyedfokú algebrai görbéken

2014. március 30.

Algebrai görbéken található számtani sorozatok kérdése egy régóta vizsgált számelméleti probléma. Különböző görbék pontjainak \(x\)- illetve \(y\)-koordinátáiból felépíthető hosszú számtani sorozatok vizsgálata ma is aktív kutatási terület. Elliptikus görbék különféle modelljei esetében az eddig talált maximális sorozatok hossza eltérő. Vannak eredmények magasabb génuszú görbék esetében is, illetve Pell-egyenletekre is vizsgálták a kérdést. Mi ebbe a sorozatba kapcsolódunk be, először egy speciális negyedfokú család esetében próbálunk felső korlátot nyerni a maximális sorozatok hosszára. Pontosabban a véges sorozatok esetében a maximumra nyerni egy felső korlátot, mert ahogyan kiderült bizonyos esetekben előfordulhat, hogy az egyenlet pontjai egy konkrét végtelen számtani sorozatot is tartalmazhatnak. A vizsgálathoz első lépésben numerikus eredményeket gyűjtünk, amelyek alapján próbálunk elméleti eredményeket is igazolni. Az \[ x^4+2x^3y+3x^2y^2+2xy^3+y^4+6x^3+12x^2y+12xy^2+6y^3-x^2+8xy-y^2-28x-28y+22=z^2 \] 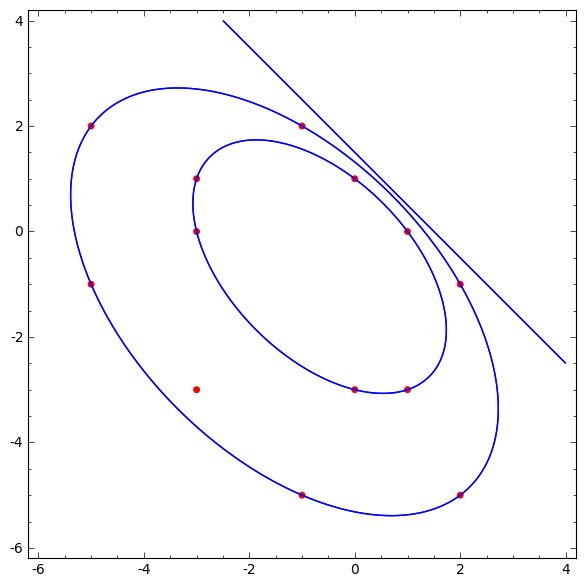egyenlet esetében végtelen hosszú sorozat nem léphet fel. Található viszont két nem triviális véges sorozat is: \[ [[-5, -3, -1, 1], [-1, 0, 1, 2]]. 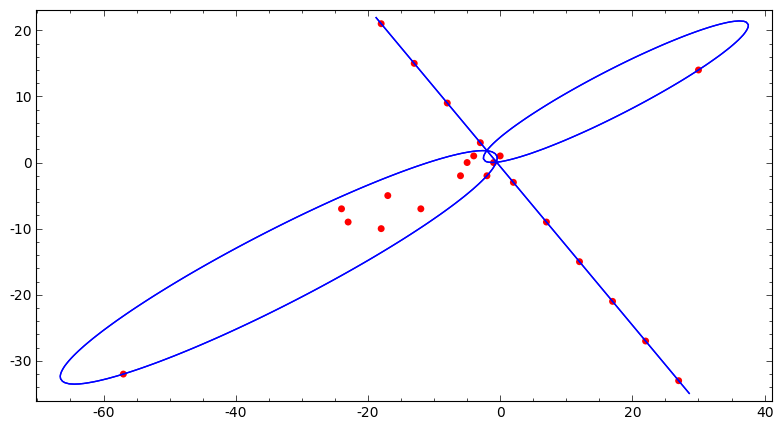\] A \[ 4x^4-28x^3y+77x^2y^2-98xy^3+49y^4+56x^3-276x^2y+476xy^2-280y^3+228x^2-672xy+512y^2+206x-335y+55=z^2 \] egyenletnél az \(x=5t-3\) sorozat esetében mindig megoldásokat kapunk, tehát ebben az esetben kapunk egy végtelen sorozatot. Véges sorozatokból pedig a következő pár megoldás létezik: \[ [[-2, -1, 0], [-6, -5, -4], [-6, -4, -2, 0], [-24, -18, -12, -6, 0], [-23, -12, -1], [-24, -12, 0]] \]

2014 április

Erdős-Graham problémával kapcsolatos cikk

2014. április 28.

Néhány apró módosítás megtétele után közlésre elfogadták Varga Nórával közös cikkünket a Glasnik Matematicki matematikai folyóiratban.

2014 május

Diofantikus és Kriptográfiai Napok

2014. május 28.

Az idei évben Szlovákiában került megrendezésre a hagyományos Diofantikus és Kriptográfiai Napok konferencia. Komárnoban a Selye János Egyetem adott otthont a rendezvénynek, melynek keretében 15 tudományos előadást hallgathattunk meg. Én a kutatási témámmal kapcsolatban az algebrai görbéken található számtani sorozatokról beszéltem, pontosabban a Huff görbéken és a Hessian görbéken az egész pontokból álló számtani sorozatokról.

2014 június

Rekurzív sorozatok és végtelen összegek

2014. június 26.

A Fibonacci sorozat igen sok összefüggésben előkerült a tudomány több területén is. A definíciója a következő: \(F_0=0, F_1=1, F_n=F_{n-1}+F_{n-2}, n\geq 2\), azaz a sorozat új eleme az előző kettő összege. Stancliff 1953-ban egy igen érdekes észrevételt tett az \(F_{11}=89\) számmal kapcsolatban: \[ \frac{1}{F_{11}}=\frac{1}{89}=0.0112358\ldots=\sum_{k=0}^{\infty}\frac{F_k}{10^{k+1}}. \] A fenti azonosságot később sokan általánosították, például Long igazolta, hogy \[ \frac{1}{9899}=\sum_{k=0}^{\infty}\frac{F_k}{10^{2(k+1)}} \] és \[ \frac{1}{109}=\sum_{k=0}^{\infty}\frac{F_k}{(-10)^{k+1}}. \] De Weger vizsgálta milyen más rendszerben kapható azonosság, Thue egyenletekre vezette vissza a problémát és Baker-módszer segítségével meghatározta az egész megoldásokat. A megoldásokból adódott, hogy \[\frac{1}{F_1}=\frac{1}{F_2}=\frac{1}{1}=\sum_{k=1}^{\infty}\frac{F_{k-1}}{2^k}\] \[\frac{1}{F_5}=\frac{1}{5}=\sum_{k=1}^{\infty}\frac{F_{k-1}}{3^k}\] \[\frac{1}{F_{10}}=\frac{1}{55}=\sum_{k=1}^{\infty}\frac{F_{k-1}}{8^k}\] \[\frac{1}{F_{11}}=\frac{1}{89}=\sum_{k=1}^{\infty}\frac{F_{k-1}}{10^k}.\] De Weger eredményét sikerült általánosítani tetszőleges bináris rekurzió esetében eljárást adtunk az \[\frac{1}{U_n}=\sum_{k=1}^{\infty}\frac{U_{k-1}}{x^k}\] egyenlet összes \(n,x\) megoldásának meghatározására, ahol \(U_0 = 0, U_1 = 1 \mbox{ és } U_n = PU_{n-1}\pm U_{n-2},\mbox{ ha } n\geq 2.\) Például igazoltuk, hogy \[\frac{1}{U_{10}}=\frac{1}{416020}=\sum_{k=0}^\infty\frac{U_k}{647^{k+1}},\] ha \(P=4.\)

2014 július

Numeration and Substitution 2014

2014. július 17.

Debrecenben került megrendezésre a "Numeration and Substitution" konferencia július 7 és 11 között. A konferencia nyitónapján délután tartottam előadást Lucas sequences and infinite sums címmel. Az előadásom a júniusi blog bejegyzésben tárgyalt témáról szólt.

2014 augusztus

On the Lucas sequence equation \(\frac{1}{U_n}=\sum_{k=1}^{\infty}\frac{U_{k-1}}{x^k}\)

2014. augusztus 15.

Közlésre elfogadták a bináris rekurzív sorozatokkal kapcsolatos végtelen összegekről szóló cikkemet. A júniusi blog bejegyzésben írtam a problémáról részletesebben.

2014 szeptember

Erdős-Graham probléma és Egész pontok Hessian és Huff görbéken publikációk

2014. szeptember 26.

Közlésre benyújtásra került két publikáció, az első az Erdős-Graham probléma egy megoldatlan részével kapcsolatos. Az \[x(x+1)(x+2)(x+3)(x+k)(x+k+1)(x+k+2)(x+k+3)=y^2\] egyenlet esetében a sejtés az, hogy csak véges sok egész megoldás létezik. A másik cikkben Hessian görbék \[H_d:\quad x^3+y^3-dxy+1=0\] esetében adunk felső korlátot az egész megoldásokra, továbbá leírást adunk a Huff görbék \[H_{a,b}:\quad x(ay^2-1)=y(bx^2-1)\] egész pontjairól. Vizsgáljuk az ilyen típusú görbék egész pontjai segítségével felépíthető számtani sorozatokat is.

2017 április

An implementation of Runge's method for Diophantine equations

2017. április 10.

The following SageMath code computes the integral solutions of the Diophantine equation \(F(x,y)=0\), the algorithm is based on the manuscript Beukers-Tengely.