Section 3 The RSA algorithm
RSA is a widely used public key cryptosystem developed by Rivest, Shamir and Adleman in 1977. The security of the RSA algorithm is based on the complexity of factorization of (large) integers. The algorithm consists of the following steps.
-
Key generation: one generates two large prime numbers \(p\) and \(q\) and computes \(N=pq,\) finally picks \(e\) such that \(\gcd(e,\varphi(N))=1.\) We remark that \(\varphi()\) is a multiplicative function and for a prime number \(p\) one has that \(\varphi(p)=p-1,\) hence \(\varphi(N)=\varphi(pq)=\varphi(p)\varphi(q)=(p-1)(q-1).\) By using the extended Euclidean algorithm one can determine \(d\) satisfying
\begin{equation*} ed\equiv 1\pmod{\varphi(N)}. \end{equation*}The public key is given by \((N,e)\) and the private key is \((p,q,d).\)
-
Encryption: for a given public key \((N,e)\) and \(x\in\mathbb{Z}_N\) one computes
\begin{equation*} \mbox{Enc}_{(N,e)}(x)=x^e\pmod{N}. \end{equation*} -
Decryption: given the private key and an encrypted message \(y\in\mathbb{Z}_N\) one determines the message as follows
\begin{equation*} \mbox{Dec}_{(p,q,d)}(y)=y^d\pmod{N}. \end{equation*}
To show that the above procedure works correctly we need to prove that
We use the following well-known result from elementary number theory.
Theorem 3.1. Fermat’s little theorem.
Let \(p\) be a prime number and \(a\) is an integer such that \(\gcd(a,p)=1.\) One has that
First we prove that \(x^{ed}\equiv x\pmod{p}.\) Since \(ed\equiv 1\pmod{\varphi(N)}\) one has that \(ed=1+k\varphi(N)=1+k(p-1)(q-1)\) for some integer \(k.\) We have that
If \(p\) divides \(x,\) then it is clear that the \(x^{ed}\equiv x\pmod{p}.\) If \(p\) does not divide \(x,\) then by Fermat’s little theorem it follows that \(x^{p-1}\equiv 1\pmod{p},\) thus
Repeating the above steps with \(q\) instead of \(p\) one obtains that \(x^{ed}\equiv x\pmod{q}.\) Since \(p\) and \(q\) are distinct prime numbers and both divides \(x^{ed}-x\) we get that \(p\cdot q=N\) divides \(x^{ed}-x,\) that is \(x^{ed}\equiv x\pmod{N}.\) To see how the RSA algorithm works in practice we provide a SageMath code.
Subsection 3.1 Common modulus attack
Suppose that at a company it is decided that they will use the RSA cryptosystem with a given modulus \(N\) and each employee will have a personalized public encryption exponent \(e\) and corresponding private decryption exponent \(d.\) A manager sends the same message \(m\) to two of his/her colleagues. It will yield two different ciphertexts
Here \(N,e_1,e_2,c_1\) and \(c_2\) are all known and one can read the secret message without knowing one of the private keys \(d_1,d_2.\) The approach is based on the extended Euclidean algorithm. We compute \(s\) and \(t\) for which
The above system of congruences provide that
It follows that
Subsection 3.2 Iterated encryption attack
This attack is based on Euler’s theorem, a generalization of Fermat’s little theorem.
Theorem 3.3. Euler.
Let \(N\) be a positive integer and \(M\) is an integer such that \(\gcd(M,N)=1.\) We have that
Suppose we use the RSA cryptosystem with the public key \((N,e)\) and we would like to send a message \(m<N.\) We need to compute \(c_1\equiv m^e\pmod{N}.\) One can consider an iterative sequence given by
This sequence is simply \(c_k\equiv m^{e^k}\pmod{N}.\) If \(\gcd(N,m)\neq 1,\) then we can easily obtain a non-trivial divisor of \(N.\) Otherwise we may apply Euler’s theorem to get that \(m^{\varphi(N)}\equiv 1\pmod{N}.\) Since \(\gcd(e,\varphi(N))=1,\) we obtain that for some integer \(k_0\) we have
Thus we get that \(c_{k_0}=m.\)
Subsection 3.3 Low public exponent attack
In the RSA cryptosystem the encryption process might be quite costly if the public exponent \(e\) is large. It may be a problem in terms of time and battery power on some limited devices like smart cards. In these cases one might choose a small public exponent like \(e=3.\) Suppose that Alice is going to send the same message to Bob, Chris and David, say \(m.\) She knows the public keys of Bob, Chris and David, let us denote these by \(N_B,N_C\) and \(N_D.\) Alice computes the ciphertexts as follows
Assume that Eve, an eavesdropper, obtains these ciphertexts. Let us see how to recover \(m.\) If \(N_B,N_C\) and \(N_D\) are not pairwise relatively prime numbers, then Eve can factor at least two of them and easily computes the private keys. So we may assume that those numbers are pairwise relatively prime. In this case Eve applies the Chinese Remainder Theorem to determine \(c\) for which \(c\equiv m^3\pmod{N_BN_CN_D}.\) Since \(m\) is less than \(N_B,N_C\) and \(N_D,\) we get that \(m^3<N_BN_CN_D.\) Thus instead of a congruence we have equality over the integers, that is \(c=m^3.\) Taking the cubic root of \(c\) over the integers yields the message \(m.\)
Subsection 3.4 Wiener's attack
If the private exponent \(d\) is small compared to \(N,\) then there is an attack based on continued fractions. A finite continued fraction is defined as follows. Let \(a_0\in\mathbb{Z}\) and \(a_1,a_2,\ldots,a_n\in\mathbb{N}.\) The expression
is called a finite continued fraction. Clearly, \([a_0;a_1,a_2,\ldots,a_n]\) defines a rational number. If \(u/v= [a_0;a_1,a_2,\ldots,a_n],\) then the rational numbers
are called the convergents to the number \(u/v.\) For a given rational number \(u_0/v_0\) with \(\gcd(u_0,v_0)=1\) the expansion can be computed via the Euclidean algorithm as follows
and \(u_n=a_n.\) For example in case of \(1234/2019\) we have
and the convergents are given by
| \(\left[0\right]\) | \(\left[0, 1\right]\) | \(\left[0, 1, 1\right]\) | \(\left[0, 1, 1, 1\right]\) | \(\left[0, 1, 1, 1, 1\right]\) | \(\left[0, 1, 1, 1, 1, 2\right]\) | \(\left[0, 1, 1, 1, 1, 2, 1\right]\) |
| \(0\) | \(1\) | \(\frac{1}{2}\) | \(\frac{2}{3}\) | \(\frac{3}{5}\) | \(\frac{8}{13}\) | \(\frac{11}{18}\) |
| \(\left[0, 1, 1, 1, 1, 2, 1, 36\right]\) | \(\left[0, 1, 1, 1, 1, 2, 1, 36, 1\right]\) | \(\left[0, 1, 1, 1, 1, 2, 1, 36, 1, 2\right]\) |
| \(\frac{404}{661}\) | \(\frac{415}{679}\) | \(\frac{1234}{2019}\) |
.
In case of rational numbers we have the classical result.
Theorem 3.6.
Let \(a,b,u,v\in\mathbb{Z}\) such that \(\gcd(a,b)=\gcd(u,v)=1\) and \(1\leq b\leq v.\) If
then \(a/b\) is a convergent of \(u/v.\)
If the private exponent \(d\) is small, then one can efficiently determine the factorization of \(N,\) a result due to Wiener.
Theorem 3.7. Wiener.
Let \(N=pq\) with primes \(p,q\) satisfying \(q<p<2q.\) Let \(d<1/3N^{1/4.}\) Given a public key \((N,e)\) with \(ed-1=k\varphi(N)\) one has
We have that \(N=pq>q^2,\) that is \(q<\sqrt{N}.\) It follows that \(0<N-\varphi(N)=p+q-1<3q<3\sqrt{N}.\) Let us consider some approximations of \(e/N.\) We obtain that
Since \(e<\varphi(N)\) and \(k\varphi(N)=ed-1<ed\) we get that \(k<d<1/3N^{1/4}.\) Hence it follows that
This is a very efficient algorithm for recovering the private exponent \(d.\) By the classical approximation relation we know that \(k/d\) is a convergent. It remains to determine which convergent’s denominator is the secret key. One encrypts a phrase using the public key \((N,e)\) and tries to decrypt it using \(N\) and the denominator of a convergent. Knowing \(d\) yields the value of \(k\) and from \(e,d\) and \(k\) one can easily compute \(\varphi(N)\) and thus \(p\) and \(q.\) The following SageMath implementation determines \(d,p\) and \(q,\) that is the private key.
Subsection 3.5 Davida's attack
This special attack due to Davida depends on the possibility to get access to recipient’s garbage. The basic idea is that the attacker intercepts a ciphertext \(c\) and transforms it. The transformed ciphertext will be meaningless when the receiver decrypts it. Therefore it will be discarded. The attacker can recover the original plaintext from the discarded one in a clever way. The steps of this attack are given below.
The attacker knows the public key of Alice, let say \((N,e)\) and also gets a ciphertext message \(c\) sent to Alice.
-
The attacker uses an arbitrary number \(k\) and determines
\begin{equation*} c_1\equiv c\cdot k^e\pmod{N}. \end{equation*}This \(c_1\) will be sent to Alice as a ciphertext.
-
Alice uses her private key \(d\) to recover the plaintext that is she computes
\begin{equation*} m_1\equiv c_1^d\pmod{N}. \end{equation*}It is very likely to be a meaningless message, hence Alice will discard it.
-
The attacker accesses the discarded plaintext \(m_1\) and computes
\begin{equation*} m_1\cdot k^{-1}\equiv c_1^d\cdot k^{-1}\equiv c^d\pmod{N}. \end{equation*}Thus the attacker will know \(c^d\pmod{N}\) corresponding to the original message.
Subsection 3.6 Elliptic curve factorization
As we saw RSA cryptography is based on the difficulty of factoring large integers. There are many algorithms that can factor very large numbers of a certain form, however general purpose efficient algorithm is still unknown. Now we introduce Lenstra’s elliptic curve factorization method.
An elliptic curve over a field \(K,\mbox{char}{K}\neq 2,3\) is given by as follows
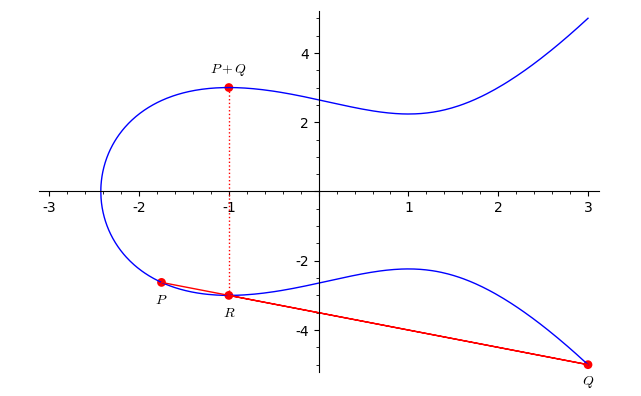
together with a point denoted by \(O,\) the so-called point at infinity. Let us see how to define a group law in a special case. Given two points \(P\) and \(Q\) on an elliptic curve over \(\mathbb{R}\) we define \(P+Q\) as the mirror image respect to the \(X\)-axis of the third intersection of the straight line passing through \(P\) and \(Q.\) As a concrete example consider the elliptic curve defined by
The third intersection point of the curve and the line is \(R=(-1,-3).\) Therefore \(P+Q=(-1,3).\)
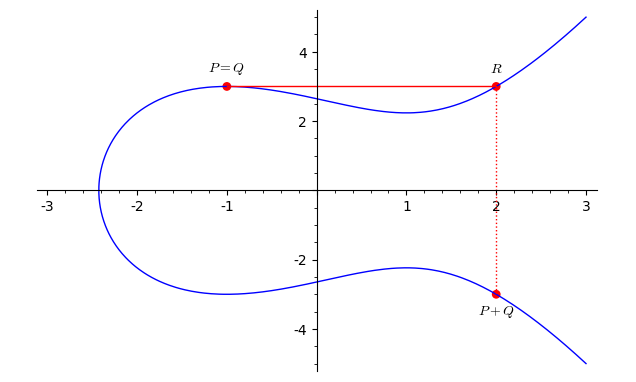
If \(P=Q\) we consider the tangent line. If \(P= (x,y)\) we define \(-P= (x,-y)\) and we have \(P+(-P)=0, P+O=O+P=P.\) Let us see this construction in case of the previously defined elliptic curve with the point \(P=(-1,3).\) In this case \(R=(2,3),\) hence \(P+P=2P=(2,-3).\)
By means of the geometric interpretation we may provide the sum of the two points \(P=(x_1,y_1), Q=(x_2,y_2)\) as
where \(m=\frac{y_2-y_1}{x_2-x_1}\) if \(P\neq Q,\) \(m=\frac{3x_1^2+a}{2y_1}\) if \(P=Q\) and \(x_3=m^2-x_1-x_2.\) Lenstra’s elliptic curve factorization method consists of computing \((B!)P\) on an elliptic curve \(E\pmod{N}\) for some given point \(P\) and given integer \(B.\) If an error arises in the group law then it can be used to factor \(N.\) The advantage of the method is that we can change the point and also the elliptic curve if no error arises.
In this example we have \(N=121932633334857493\) and it turns out that that the elliptic curve factorization algorithm works, for example taking the curve \(y^2=x^3+49x+1\) and the point \(P=(0,1)\) we obtain that \(N\) is divisible by 123456791, in fact
Subsection 3.7 Continued fraction factorization method
It was the first integer factoring algorithm with a sub-exponential running time. The basic idea behind the algorithm is that if we have two integers \(x\) and \(y\) for which
then \(N\) divides \(x^2-y^2=(x-y)(x+y)\) and there is a chance that \(\gcd(N,x-y)\neq 1\) or \(\gcd(N,x+y)\neq 1.\) So we compute the continued fraction expansion of \(\sqrt{N}\) and the convergents, denoted by \(P_n/Q_n\) for an integer \(n.\) Here we have that
It follows that \(C_n=P_n^2-NQ_n^2\) is relatively "small", a fact that can be used to search for numbers having only small prime divisors. We clearly have that \(C_n\equiv P_n^2\pmod{N}.\) We generate congruences for which \(C_n\) has only prime divisors less than or equal \(B\) (these are the so-called B-smooth numbers) for some fixed integer \(B.\) That is we obtain
for \(i=1,2,\ldots,s.\) We would like to determine a subset \(S\) of \(\{1,2,\ldots,s\}\) such that
where \(p^{\sum_{i\in S}a_{i,p}}\) is even for all \(p<B.\) This latter part is linear algebra modulo 2. In SageMath a possible implementation is as follows.
Subsection 3.8 Dixon's method
The continued fraction factorization method is a variant of Dixon’s algorithm, the only difference is the way to obtain appropriate congruence relations. Here we take a sequence \(x_n\) of distinct random integers for which \(\sqrt{N}<x_n<N.\) We search for congruences
for \(i=1,2,\ldots,s,\) where \(B\) is a bound for the element of the factor base like in case of the continued fraction factorization.
Subsection 3.9 Pollard's \(\rho\) factorization
John Pollard in 1975 introduced a factorization method in the article "A Monte Carlo method for factorization". This factorization algorithm is based on congruences using a polynomial and involves some probabilistic ideas. Brent and Pollard applied this method to factor the eighth Fermat number
Let us describe the algorithm to factor an integer \(N\text{.}\) Let \(f(x)\) be a polynomial (usually we take \(f(x)=x^2+c\) for some integer \(c\)). We define two sequences \(x_n\) and \(y_n\) as follows. Let \(x_0=y_0=2\) and
We iterate these sequences until
If \(g<N,\) then we determined a non-trivial divisor of \(N\) (since by construction \(g>1\)). Otherwise the procedure fails, we get that \(g=N.\) In case of \(N=6557\) we have
| \(x_n\mod N\) | \(x_n\mod 79\) | \(y_n\mod 79\) |
| \(2\) | \(2\) | \(2\) |
| \(5\) | \(5\) | \(26\) |
| \(26\) | \(26\) | \(51\) |
| \(677\) | \(45\) | \(26\) |
| \(5897\) | \(51\) | \(51\) |
| \(2839\) | \(74\) | \(26\) |
| \(1369\) | \(26\) | \(51\) |
| \(5417\) | \(45\) | \(26\) |
| \(1315\) | \(51\) | \(51\) |
| \(4735\) | \(74\) | \(26\) |
| \(1843\) | \(26\) | \(51\) |
.
Since there are only finitely many possible values modulo 79 the two sequences \(x_n\) and \(y_n\) will cycle. For example we see that \(x_n\pmod{79}\) will follow the graph given below. We also see that \(x_4\equiv y_4\pmod{79}\) and the method gives that
SageMath summary.
- IntegerRing()
Returns the integer ring.
- Integers()
Returns the integer ring.
- ceil()
The ceiling function.
- continued_fraction()
Returns the continued fraction.
- convergents()
Returns the (partial) convergents of a number.
- denominator()
Returns the denominator of a fraction.
- digits()
Returns the digits of a number in a given base.
- dimension()
Returns the dimension.
- is_prime()
Returns true if the number is prime, false otherwise.
- is_unit()
Returns true if the element is a unit.
- next_prime()
Returns the next prime number.
- nth_root()
Returns the (possibly truncated) \(n\)-th root.
- numerator()
Returns the numerator of a fraction.
- power_mod()
Returns the \(n\)-th power of \(a\) modulo the integer \(m.\)
- right_kernel()
Computes the space of vectors \(w\) so that \(A\cdot w=0.\)
- solve()
Solves certain types of equations/systems of equations.
- sqrt()
Returns the square root of an element.
- transpose()
Returns the transpose of a matrix.
- valuation()
Returns the valuation.
Exercises 3.10 Exercises
1.
In RSA we have \((n,e)=(5352499,3516607).\) Encrypt the message "The only way to learn mathematics is to do mathematics".
2.
In RSA we know \((p,q,d)=(12227,35569,136215539),\) and we receive the encrypted message
Determine the original message.
3.
Factor the integer \(N=5352499\) by using elliptic curves.
4.
Factor the integer \(N=5352499\) by using continued fractions.
5.
Factor the integer \(N=5352499\) by applying the quadratic sieve.
6.
Factor the integer \(N=5352499\) by applying Pollard’s \(\rho\) algorithm with 2 different quadratic functions.
7.
In RSA we know \((N,e_1,e_2,c_1,c_2)=(8137,7,23,7155,2626).\) Apply the common modulus attack to recover the secret message.
8.
In RSA apply the iterated encryption attack to obtain a list containing the possible values of the secret message. We have that \((N,e,c)=(1591,5,22).\)
9.
In RSA we have \((N,e)=(24739307, 7526327).\) Apply Wiener’s attack to recover the secret key \(d.\)
10.
Bob, Chris and David have RSA public keys given by \((N_B,e_B)=(6527,7), (N_C,e_C)=(11537,7)\) and \((N_D,e_D)=(10123,7),\) respectively. Alice sends the same message to both of them, the ciphertexts are as follows \(c_B=2268, c_C=3442\) and \(c_D=4737.\) Determine the message by means of the low public exponent attack.
