7. hét    Ciklusszervező utasítások

Tartalom:

    7.1. Előfeltételes ciklus: while
    7.2. Előfeltételes ciklus: for    
    7.3. Végfeltételes ciklus: do .. while
    7.4. Ciklusok egymásba ágyazása
    7.5. Alapvető algoritmusok
        7.5.1. Megszámlálás
        7.5.2. Összegzés, átlagszámítás
        7.5.3. Minimum- és maximum kiválasztás
    7.6. Tesztkérdések
    7.7. Feladatok

Ha egy bizonyos tevékenységet a programban egymásután többször végre kell hajtani, akkor ciklusokat alkalmazunk. A ciklusok végrehajtását, vagy az abból való kilépést feltételekhez kötjük.

Egy ciklus általános felépítése:
                · fej
                · mag
                · vég

Az ismétlésre vonatkozó információk vagy a fejben vagy a végben találhatók.

A magban helyezzük el azokat az utasításokat, amelyeket többször végre akarunk hajtani.

A ciklusok működése során két szélsőséges esettel is találkozhatunk:
                · Üres ciklus: A ciklusmag egyszer sem fut le.
                · Végtelen ciklus: Az ismétlődés soha nem áll le.

7.1.   Előfeltételes ciklus: while

Működési elv:

A program a ciklusba való belépés előtt megvizsgálja a feltételt (belépési feltétel), és ha ez teljesül, akkor a ciklusmag végrehajtásra kerül, egyébként nem. Ennél a ciklus fajtánál kialakulhat üres ciklus, abban az esetben, ha a belépési feltétel soha nem teljesül.

Példa: (Írjunk ki a konzolra egymásmellé 6 db csillagot!)

7.2.   Előfeltételes ciklus: for

Működési elv:

inicializálás: Itt deklaráljuk a ciklusváltozót, és adjuk meg annak kezdeti értékét.

feltétel: Belépési feltétel, minden ciklus elején kiértékelődik, ha igaz, akkor a ciklus végrehajtásra kerül, egyébként a vezérlés a for utáni utasításra ugrik.

növekmény: Itt változtatjuk meg a ciklusváltozó értékét.

Példa:

A for fejének tagjai hagyhatók üresen is, de a pontosvesszőket ki kell tenni. pl. for(;;)...

7.3.   Végfeltételes ciklus: do..while

Működési elv:

A ciklus magja egyszer mindenképpen végrehajtódik, majd a ciklus végén, egy feltételvizsgálat következik, amely eldönti, hogy bent maradunk-e a ciklusban, vagy nem. Ha a feltétel igaz, akkor a ciklusmag újból végrehajtásra kerül. Ez a folyamat addig folytatódik, amíg a feltétel hamissá nem válik (bennmaradási feltétel).

Üres ciklus a végfeltételes ciklusnál nem fordulhat elő, hiszen a ciklus magja legalább egyszer lefut.

Példa:

Az előző három ciklus mindegyike ugyanazt a feladatot oldotta meg, kirajzolt 6 db csillagot a képernyőre.

7.4.   Ciklusok egymásba ágyazása

A ciklusainkat egymásba is ágyazhatjuk.

Nézzünk meg egy egyszerű példát két ciklus egymásba ágyazására!

Példa:(Jelenítsük meg a konzolon következő alakzatot: ********************
                                                                              ********************
                                                                              ********************)

Forrásprogram:

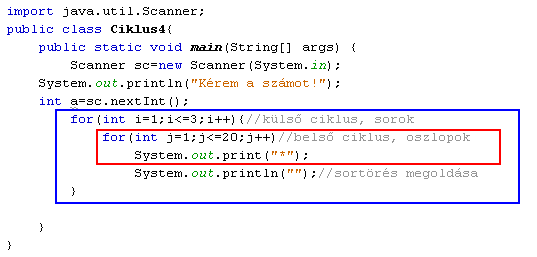
A program elemzése:

A csillagok egy 3 soros, 20 oszlopos táblázatot alkotnak. A kirajzolást úgy tudjuk egyszerűen elképzelni, mintha a táblázat celláiba helyeznénk el a csillagokat.

A külső ciklusban megyünk végig a sorokon, a belső ciklusban pedig az oszlopokon. Először az 1. sor elemeit jelenítjük meg egymásután, majd a 2. sor elemeit, és végül a 3. sor következik. Ha egy teljes sort megjelenítettünk, akkor meg kell oldani a sorváltás problémáját. Ezt egyszerűen egy println("") utasítással is megtehetjük.

7.5. Alapvető algoritmusok

7.5.1. Megszámlálás

Ezzel az algoritmussal egy sorozat, adott tulajdonsággal rendelkező elemeit számoljuk meg.

Az algoritmus menete a következő:

1.    A számlálót nullára állítjuk.

2.    Végig lépkedünk a sorozat elemein és ha az aktuális elem tulajdonsága megegyezik az adott tulajdonsággal, akkor a számláló értékét egyel megnöveljük.

3.    Megjelenítjük a számláló értékét, ez a szám adja az adott tulajdonsággal rendelkező elemek számát.

Példa: ("Ma süt a nap." sztringben megszámoljuk az 'a' karakterek számát.)

 

 

 

7.5.2. Összegzés, átlagszámítás

Az olyan feladatokat, amelyekben a sorozat elemeit valamilyen módon gyűjtenünk kell (pl. göngyölítés) összegzéses feladatoknak nevezzük. Ebbe a feladatcsoportba sorolható a különbség-, illetve a szorzatképzés is.

Átlag kiszámításakor egyszerre két dolgot is végzünk - összegzünk, s közben számlálunk is. Végül a két érték hányadosát vesszük.

Példa: (Addig olvassuk be a számokat, amíg 0-t nem ütünk, majd írjuk ki a számok összegét és átlagát!)

Figyelem: Az átlag számításakor vigyázni kell a 0-val való osztásra!

7.5.3. Minimum- és maximum kiválasztás

Minimumkiválasztás esetén a sorozat legkisebb, maximumkiválasztás esetén a sorozat legnagyobb elemét kell meghatároznunk.

Az algoritmus menete a következő:

1.    A sorozat első elemét elhelyezzük egy minimum(maximum) változóba.

2.    Sorban végig lépkedünk az elemeken és ha az adott elem kisebb(nagyobb) a minimum(maximum) változóban lévőnél, akkor a változóba lévő elemet kicseréljük vele.

3.    Megjelenítjük a változóban található elemet, ez az elem lesz a sorozat minimuma(maximuma).

 

Példa: (A program bekér 5 db valós számot, majd megjeleníti a legkisebbet!)

7.6.    Tesztkérdések

7.7.    Feladatok

7.7.1.    Készíts programot, amely egymás alá hússzor kiírja a "Jó napot kívánok!" szöveget! (megoldás)

7.7.2.    Készíts programot, amely 1-től 10-ig kiírja egymásmellé, vesszővel elválasztva a számok négyzetét! (megoldás)

7.7.3.    Írjál programot, ami 50 db kockadobást szimulál, és kiírja a dobásokat egymás mellé, szóközzel elválasztva! (megoldás)

7.7.4.    Írjuk ki az 1-200 közötti számok közül azokat az 5-tel oszthatóakat, amelyek nem oszthatók 25-tel! (megoldás)

7.7.5.    Kérd be n értékét és készítsd el az alábbi n soros háromszöget!
minta:
1
1    2
1    2    3
.     .     .
1    2    3    n

(megoldás)